Accumu Vol.25
古を語る星ぼし⑦暦の計算法

京都情報大学院大学教授 作花 一志
はじめに
私たちの毎日の生活は暦を基にしています。○月〇日の記録や予定,学校の授業時間割やTVの番組は曜日単位ですね。
暦に使う時の単位として1日は地球の自転周期が元になっていますが,地球の公転周期は365.242194・・・日。しかし実際の暦ではこのような端数は使えないので現行暦では365.2425日としています。この値をずっと使い続けると毎年この差0.0013日だけ誤差が出てきて,すなわち3300年経つと1日の誤差が出てくることになります。現行暦が施行されたのは(国によって異なりますが)1582年からでまだ500年しか経っていないので,当面不自由はありませんが,もっと正確な暦はできないものでしょうか?
私たちの祖先はどうやって時を知り,暦を作ったのでしょうか?狩猟採集生活をしている時代には暦は要らなかったでしょう。山に行って木の実を採り,川や海に行って魚を取り,森や草原で獣を捕らえ・・の時代には。それでも雪が解け,花が咲き,山が紅葉に染まるのがある一定周期で繰り返されることを知り,それが太陽や月の運行によるものと理解していきました。農業を始めると種まき刈り入れの時期の知識が必要になって来ます。季節の巡り,植物の生長から1年という周期を知り星の運行から単位で浮き暦の発祥は文明の興りと同じく世界のあちこちのを作った民族また暦は占い迷信と深い関係があります。
- 13日金曜は不吉な日
- 葬儀は友引の日は避ける
- 丙午の女性はなんとやら
- ヘビ年,さそり座の生まれの人は嫌われる,などなど。
暦には太陽暦,太陰暦,太陽太陰暦の3種類あります。私たちが現在使っているのは太陽暦で,太陽の運行を基にして作られ月の満ち欠けには無関係です。この号では太陽暦の解説をします。最も複雑で巧妙な太陽太陰暦については次号でお話しします。
なおこの小文はアキューム14号に掲載した文章を加筆修正したものです。
太陽暦と閏年
現在私たちが使っている暦のルーツはエジプトです。ナイル川は毎年決まった時期になると洪水を起こし,そのときは避難しなければなりませんが,同時に上流から肥沃な土を運んでくるので耕作には欠かせません。その時期は東北から太陽が昇ってくる直前に東南からシリウスが昇ってくるころ,その周期は365と1/4日いうことを彼らは気づいていました。その暦はユリウス・カエサル(シーザー BC100-BC44)によってローマにもたらされ(BC45年),閏年設置をつけて
- ●1年=365日であるが4年に1度,閏年を設け,366日とする
- ●年初はMartiusからJanuarisに変更する
- ●奇数月の日数は31日,偶数月は30日とする。ただしFebruariusのみ平年は28日で閏年は29日とする。これは古代ローマ暦ではFebruariusが年末だった風習を引き継いだためです。カエサルは自分の誕生月の名前をJuliusに変えましたが,後継者アウグストゥス(BC63-AD14)も自分の誕生月の名前をAugustusに変え,さらにその月の日数を31日に,それ以降の月の日数も変えてしまいました。これをユリウス暦(表1)といいローマ帝国全体に定着しました。
| 月 | 英語 | 古ローマ | 古代ローマの月名の由来 | 日数 |
|---|---|---|---|---|
| 1月 | January | Ianuarius | 過去・未来を見据えて門を守る神ヤヌスに由来 | 31 |
| 2月 | February | Februarius | 浄罪と贖罪の神フェブアリウスに由来 | 29 |
| 3月 | March | Martius | 軍神マルスに由来 | 31 |
| 4月 | April | Aprilis | 美と愛の女神アフロディテに由来 | 30 |
| 5月 | May | Maius | 豊穣の女神マイアに由来 | 31 |
| 6月 | June | Iunius | 結婚の女神ユーノーに由来 | 30 |
| 7月 | July | Quintilis | 5番目の月ユリウス・カエサルをたたえてIuliusに改称 | 31 |
| 8月 | August | Sextilis | 6番目の月アウグストゥスをたたえてAugustusと改称 | 30 |
| 9月 | September | September | 7番目の月 | 31 |
| 10月 | October | October | 8番目の月 | 30 |
| 11月 | November | November | 9番目の月 | 31 |
| 12月 | December | December | 10番目の月 | 30 |

図1 ユリウス・カエサル
ユリウス暦では単純に西暦が4で割リ切れる年はすべて閏年としていました。1400年も1500年も閏年です。ユリウス暦では4年に1度,1年を366日としているので,1年の平均日数は365+1/4=365.25であり,一方1年の日数は365.242194・・・日(回帰年)ですから,1年につき0.0078日の誤差が出ます。このわずかな誤差でも128年経つと1日の誤差を生みます。128歳まで生きる人はいないので日常生活にはそこまでの正確さは必要ありませんが,長期間にわたって毎年決まった日に行事を行うとなればこれでは不十分です。キリスト教の重要行事である復活祭(イースター)は基本的に「春分の日の後の最初の満月の次の日曜日」(諸説あり)ですから,春分の日を正確に決めねばなりません。ユリウス暦は非常に長期間使われていたため,春分の日は前へ前へずれていき,16世紀には3月11日になっていました。そこで当時のローマ教皇グレゴリウス13世は学者たちを招集して暦の研究を行わせ,1582年に閏年を下記のように置く新暦(グレゴリオ暦)を制定公布しました。
- ①西暦年が4で割リ切れる年は閏年
- ②ただし西暦年が100で割リ切れる年は閏年ではない
- ③ただし西暦年が400で割リ切れる年は閏年
なんだかわかりにくいですが,どの本でも大体似たような表現です。そこでプログラミングできるように少し書き換えてみます。
- ⓐ西暦年が400で割り切れる年。
- ⓑ西暦年が4で割り切れるが100で割り切れない年。
「この2つの条件のどちらかに当てはまる年は閏年,それ以外は平年」とすれば多少はスッキリします。
1582年10月4日(木曜日)の翌日は10月15日(金曜日)となったため10日間は空白となりましたが,曜日は連続しています。グレゴリオ暦は閏年を減らすために制定されたもので,閏年を400年間に400/4-400/100+400/400=97回置いているから1年の平均日数は
365+97/400=365.2425日となります。
グレゴリオ暦はローマカトリック系の国(スペイン,ポルトガル,フランス,イタリア・南ドイツ諸都市・諸国など)ではその日からあるいは翌年から採用されます。この日を生きていたガリレオの場合,生年月日はユリウス暦1564年2月15日で,没年月日はグレゴリオ暦1642年1月8日です。しかしプロテスタント系の国(イギリス,スウェーデン,北ドイツ諸国など)では約200年も遅れます。イギリスでは(植民地だったアメリカを含む)1752年からです。ニュートンの生没年は1642年12月25日〜1727年3月20日,ですがこれはユリウス暦での日付です(グレゴリオ暦では1643年1月4日〜1727年3月31日)。最も遅れるのは東方正教教会系の国(ロシア,ギリシアなど東欧)で,第1次世界大戦ころまでユリウス暦を使っていました。今も宗教行事にはユリウス暦だそうです。アジア諸国は19世紀後半~20世紀初に太陰太陽暦から太陽暦に切り換えますが,ユリウス暦は使っていません。わが国で太陽暦が採用されたのは明治六年(1873年)からとなっていますが,正確には旧暦の明治五年12月3日がグレゴリオ暦の明治六年の1月1日に変わりました。したがって明治五年12月には3日以降はなかったのです。暦を変更するために詔書(朕惟フニで始まる)および太政官布告が出ています。しかし混乱を避けるため政府が正式に認めた暦にも明治四十二年の暦まで旧暦の日付が参考として記されていたそうです。韓国では1896年から中国では1912年から,また中東では独自の太陽暦が使われています。
| 世紀 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 日数 | -2 | -1 | 0 | 1 | 1 | 2 | 3 | 4 | 4 | 5 | 6 |
| 世紀 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 日数 | 7 | 7 | 8 | 9 | 10 | 10 | 11 | 12 | 13 | 13 | 14 |
20世紀21世紀ではユリウス暦は13日遅れています。1700年,1800年,1900年はユリウス暦では閏年ですが,グレゴリオ暦では平年になったためです。13日のずれは2100年まで続きます。ユリウス暦日をグレゴリオ暦に変換するときにはユリウス暦日に表2の日数を加えます。
ところで民法によると閏年であれ平年であれ「誕生日の前日が終了する瞬間に年齢が変わることになる。」そうです。したがって2月29日生まれの場合は,2月28日が終了する瞬間に年齢が変わります。運転免許更新やいろいろな満期などにはご注意を。
グレゴリオ暦でも閏の問題は完全に解決したわけではなく3320年につき1日ずれます。1923年,それまでユリウス暦を使っていたギリシャ正教会などは改訂ユリウス暦と呼ばれる新しい暦を制定しました。
- ①西暦年が4で割り切れる年は閏年
- ②ただし西暦年が100で割り切れる年は平年
- ③ただし西暦年を900で割った余りが200または600になる年は閏年
①と②はグレゴリオ暦と同じですが,③は違っています。これによると閏年は900年間に900/4-900/100+2=218回ありますから,1年は平均365+218/900=365.242222日で,グレゴリオ暦より1桁も精度がよく,数万年もずれません。将来,2800年がグレゴリオ暦では閏年なのに対し,改訂ユリウス暦では平年になり,日付は1日ずれます。2900年は逆に改訂ユリウス暦だけが閏年となり,日付は再び一致しますが,3200年と3300年でまた同じようなことが起こります。正確ではあってもかえって複雑ですから,果たしてどこの国が使っているかは知りません。
実はこのような新しい正確な暦は簡単にできます。y年の間にx回閏年を置くと1年の平均日数は365+x/y日であり,それが1回帰年365.242194・・・日に近くなるような自然数xとyを探していきます。1000年間にわたって調べた結果が表3です。
| 年 | 回 | 1年の日数 | 差 | 備考 |
|---|---|---|---|---|
| 929 | 225 | 0.2424959 | 0.000002 | |
| 801 | 194 | 0.2421973 | 0.000003 | |
| 673 | 163 | 0.2421991 | 0.000005 | |
| 128 | 31 | 0.2421875 | -0.000006 | |
| 450 | 109 | 0.2422222 | 0.000028 | 改訂ユリウス暦 |
| 33 | 8 | 0.2424242 | 0.000230 | |
| 400 | 97 | 0.2425000 | 0.000306 | グレゴリオ暦 |
| 4 | 1 | 0.2500000 | 0.007806 | ユリウス暦 |
第1列はy,第2列はxであり,第3列はx/yの値,第4列は0.242194との差です。第3列の値が0.242~0.243となるものは1000年間に499回ありますが,そのベスト3件と参考5件を載せました。最も誤差が小さいのは閏年を929年間に225回設ける場合ですが,これを実際に設置することは困難です。2番目3番目についても同様のことがいえます。それらに比べると誤差はやや大きいが,4番目の場合は使えそうですね。128年間に31(=128/4-1)回の閏年を置くことになりますから具体的には
- ①西暦年が4で割り切れる年は閏年
- ②ただし,西暦年が128で割り切れる年は平年
とすれば実用的になりそうです。128で割り切れるとは3回続けて4で割った時の商が偶数であるということです。128で割り算を実行する必要はありません。実際に改暦が行われたら・・・近い将来の変更は①より2100年は閏年で,②より2048年は平年となります。この暦は現在イランで使われているそうです。では6番目の場合の閏年設置法を考えてみましょう。33年間に西暦年が3で割り切れる年は11回,9で割り切れる年は3回あるから

図2 ウマル・ハイヤーム
- ①西暦年が3で割り切れる年は閏年
- ②ただし,西暦年が9で割り切れる年は平年
とすればよさそうですね。2016年は平年で次の閏年は2019年になります。この置閏法による暦は『ジャラーリー暦』でセルジュック朝の天文学者・詩人であるウマル・ハイヤーム(1048年-1131年)によって作られました。彼は3次方程式の解法や2項定理などで先駆的な研究を行っています。この暦では閏年8回のうち7回は4年に一度,8回目の閏年は5年に一度,となっています。このため,変則的な閏年が頻繁にやってくることになり,あまり普及せずやがて使われなくなりました。
このように正確さからいえばグレゴリオ暦より優れた暦はいくつもありますが,実用には向かないようです。
曜日と干支の起源
曜日はいつから
v日本人はいつから日月火水木金土という曜日を使っているのでしょうか?明治になってから欧米にならった?鎖国中にオランダ商人がもたらした?戦国時代にやってきた宣教師が伝えた?いやそうではなく,もっともっと古くから曜日は使われていたのです。七曜はヨーロッパから伝わったのではなく,空海(774-835)が9世紀の初めに唐から持ち帰ったもので『宿曜経』という占星書に書かれています。藤原時代には密教行事だけでなく広く貴族間で使われていました。藤原道長(966-1028)自筆の日記『御堂関白記』には,長保六年二月十九日(=1004年3月12日)に藤原道長は84歳の安倍晴明(921-1005)を伴って,新しく作る法華三昧堂の土地探しに木幡(京都府宇治市)に行き,その日は癸酉の日曜日ということが記されています。この日が日曜であることは,実際に計算して確認されます。『御堂関白記』は陰陽師の作った「具注暦」という暦に道長自身が書き込んだもので,そこには干支・二十四節気・吉凶の占いはもちろん,日・月・火・水・木・金・土までが書いてあります。『宿曜経』にはまた白羊(おひつじ),青牛(おうし),陰陽(ふたご),巨蟹(かに),獅子(しし),小女(おとめ),秤量(てんびん),蝎虫(さそり),人馬(いて),磨羯(やぎ),宝瓶(みずがめ),雙魚(うお)という十二宮も載っていて,これらを使って宿曜師は星占いをしていたようです。
その他にも,承元四年=1210年および正和四年=1315年の「具注暦」が京都大学宇宙物理学教室図書室で見ることが出来ました。また南北朝時代の康永4年=1345年の「仮名暦」は栃木県荘厳寺に保存されています。江戸時代にはわが国初の暦を作った渋川春海(1639-1715)の署名のある貞享五年=1688年の具注暦,また大和国だけで使われていた文化十年=1813年の「南都暦」などに記載されている曜日はすべて現在の曜日に連続しています。
世界各国の曜日名と曜日の順序
英語では日曜・月曜・土曜は天体名,火曜から金曜までは北欧神話の神々の名がつけられています(表4)。Tuesdayは軍神テュールの日,Wednesdayは最高神オーディンの日,Thursdayは雷農耕の神トールの日,Fridayは美と愛の女神フレイアの日であり,ドイツ・オランダ・ノルーウェイ・スウェーデン語など北欧では一般にそうです。一方,フランス・スペイン・イタリア語などラテン系では日曜(主の日)と土曜(安息日)はキリスト教にちなむ名前で,他は天体名です。フランス語のlundi,mardi,mercredi,jeudi,vendrediはそれぞれ月ルナ(ダイアナ),火星マルス,水星メルクリウス(マーキュリ),木星ジュピター(ゼウス),金星ビーナスに由来しています。中国やイスラム系諸国(インドネシアからアフリカまで)では一般に1,2,3・・・と番号が付けられています。またスラブ系ではいろいろな要素が混入されています。すべてに天体名を使っているのはインド・タイ・日本・韓国など東アジア諸国ですが,古代ギリシアがそうであることは興味深いですね。Helios,Selenes,Areos,Hermeos,Dios,Aphrodites,Kronosは太陽,月,火星,水星,木星,金星,土星の神でありまた天体を表します。
曜日がどこで初めて使われたかは定説はないようですが,ヘルニズム時代に当時世界最大の都市アレキサンドリアで天体名で使われ始め,そこから各地に広まったと言われています。西方(ヨーロッパ)ではキリスト教その他さまざまな宗教に影響され,何回か名前が変わりましたが,東方には原型のまま伝わり,東アジアでは今も日・月・五惑星の名前がそのまま残っています。中国はかつて日本や朝鮮と同じ天体名を使っていたが(ただしあまり普及しなかった)20世紀になってから番号に変えたそうです。曜日の起こりは聖書の創世記の記述「神は6日でこの世を創造し7日目は休んだ。」ことによると言われるのは後世の挿話のようです。

図3 曜日の伝播
| 日本語 | フランス語 | 英語 | 中国語 | 古代ギリシア | ||
|---|---|---|---|---|---|---|
| 日 | dimanche | 主の日 | Sunday | 太陽の日 | 星期日 | Helios |
| 月 | lundi | 月の日 | Monday | 月の日 | 星期一 | Selenes |
| 火 | mardi | 火星の日 | Tuesday | ティルの日 | 星期二 | Areos |
| 水 | mercredi | 水星の日 | Wednesday | オーディンの日 | 星期三 | Hermeos |
| 木 | jeudi | 木星の日 | Thursday | トールの日 | 星期四 | Dios |
| 金 | vendredi | 金星の日 | Friday | フレイアの日 | 星期五 | Aphrodites |
| 土 | samedi | 安息日 | Saturday | 土星の日 | 星期六 | Kronos |

図4 曜日の順序
さて曜日の順序はどのように決められたのでしょうか?7天体の明るい順でも近い順でもなさそうです。これについては200年頃,ローマの元老院議員・執政官を務めたカシウスが著わした『ローマ史』に次のような興味ある記述があるそうです。当時すでに太陽・月・五惑星の遠近の順序は回帰周期から知られていました。その周期は月では約27日,土星では約30年です。遠い天体ほどゆっくり運動するので周期は長いというわけです。そこで遠い順に「土木火日金水月」と左から書き並べて,24で改行するということを何回か繰り返して,上から読んでみると,「日月火水木金土」の順になるというわけです。実は24でなくても7で割って3余る数なら何でもよく,最も簡単な数は10です(図4)から実際に試してみてください。
曜日の計算
Excelの関数で曜日を求める時には図5のように関数TEXTを使うと便利です。
ただし「有効なのは1900年3月1日以降であること。1899年12月31日以前では全く無効で,1900年は閏年として扱わていて1月と2月は曜日が1つずれている。」ことにご注意。

図5 Excelによる曜日の計算
19世紀以前の曜日を求めるには,割算の余りを計算する必要があります。
まず1900年1月1日(月曜)を第1日としてyy年mm月dd日までの通日Tを
T=[365.25*yy]-[yy/100]+[yy/400]+[30.59*(mm-2)]+dd-693931
で定義します。ただし[ ]は切り捨て整数化の記号で,また1月と2月は前年の13月,14月とします。そうすればTを7で割った余りが0なら日曜日,1なら月曜日,...,なら土曜日となります。
あなたは自分の干支は当然知っていますね,年齢を数ではなくて十二支で言うこともよくあります。十二支の求め方は西暦年を12で割った余りが0なら申(さる),1なら酉(とり)・・・・・11なら未(ひつじ)というように求めることができます。
| 十干 | 十二支 | 方位 | 時刻 | |
|---|---|---|---|---|
| 0 | 庚 かのえ | 申 さる | 16 | |
| 1 | 辛 かのと | 酉 とり | 西 | 18 |
| 2 | 壬 みずのえ | 戌 いぬ | 20 | |
| 3 | 癸 みずのと | 亥 ゐ | 22 | |
| 4 | 甲 きのえ | 子 ね | 北 | 0 |
| 5 | 乙 きのと | 丑 うし | 2 | |
| 6 | 丙 ひのえ | 寅 とら | 4 | |
| 7 | 丁 ひのと | 卯 う | 東 | 6 |
| 8 | 戊 つちのえ | 辰 たつ | 8 | |
| 9 | 己 つちのと | 巳 み | 10 | |
| 10 | 午 うま | 南 | 12 | |
| 11 | 未 ひつじ | 14 |
十干はあまりなじみがありませんが,年を10で割った余り,すなわち年の1の位の数で決まります。その数が0なら庚(かのえ),1なら辛(かのと)・・・・9なら己(つちのと)と。戊「つちのえ」と戌「いぬ」,己「つちのと」と巳「へび」の字は間違いやすいのでご注意を。2018を10で割ると余りは8だから十干では戊,また12で割って2余るから十二支では戌,すなわち今年2018年の干支は戊戌(つちのえいぬ)です。来年2019年は干支とも1つ進むので己亥(つちのとゐ)となります。干支は10と12の最小公倍数である60を周期として繰り返されます。
中国では干支の使用は非常に古く殷の時代の甲骨文字にも記されていました。四書五経にはもちろん,紀元前11世紀の青銅器の文字にも干支を読み取ることができます。殷周の戦いはBC1047年の初冬に始まり,最終戦である牧野(ぼくや)の戦いは「甲子の日」に行われたそうです。それはいつでしょうか?BC1046年の甲子の日は1月20日,3月21日・・・と6回ありますが,『漢書』の記載では明らかに冬ですから1月20日が最有力でしょう。さらに武王が天子に就いたのは辛亥の日といわれ同年3月8日となります。干支は東アジアの多くの民族の間で広く使われてきています。わが国では埼玉県の稲荷山古墳から出土した鉄剣に「獲加多支鹵(わかたける)大王」と「辛亥年七月」の記載があることから,これは「雄略天皇」時代の「471年」とする説が有力です。飛鳥時代には公文書に記入されていました。歴史的に有名な事件には,干支がつけられているものが少なくありません。志賀の都が滅びた壬申の乱は672年に,清朝滅亡の源となった辛亥革命は1911年に起こりました。高校野球のメッカである甲子園球場は1924年に作られました。10で割っても12で割っても余りが1(すなわち60で割って余りが1)である年は辛酉(かのととり:しんゆう)となりますが,この年は重要な始まりの年であると言われていました。辛酉の年には王朝が交代する(辛酉革命)という思想があり,推古天皇九年(601年)より1260(=60×7×3)年前の辛酉の年であるBC660年が神武天皇即位の年と定められたと言われています。最近の辛酉の年は1981年でした。
また60年たって干支が戻ってくることを還暦と言い,60歳の誕生日に赤ん坊に戻ったとして赤いちゃんちゃんこでお祝いしていますが,現在では寿命が延びて60歳はまだ元気(生臭い)なので還暦祝いを嫌がる人も少なくないようです。
干支は年だけでなく日にもつけられ,十干名は10日周期で,十二支名は12日周期で繰り返されます。60日経つと同じ干支となります。
干支については上記のTを10で割った余りが0なら甲,1なら乙,…,9なら癸です。また12で割った余りが0なら戌,1なら亥,…,11なら酉です。
2018年1月6日,3月7日,5月6日,7月5日,9月3日,11月2日は戊戌の年の戊戌の日となります。1年後2019年1月6日の干支は?365は10で割っても12で割っても余りは5だから,干も支もそれぞれ5ほど進み戊戌となります。
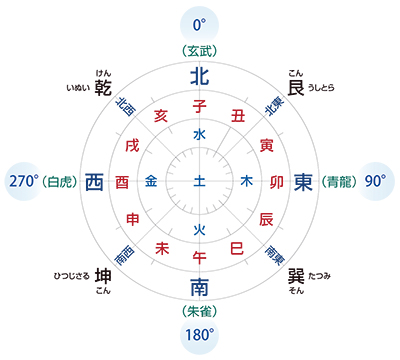
図6 干支と方位
図6のように十二支は方位を表す時にも使われます。子丑寅・・・亥を時計回りに環状に並べ北を子,東を卯,南を午,西を酉の方位としました。それらの中間の北東は艮(うしとら),南東は巽(たつみ),南西は坤(ひつじさる),北西は乾(いぬい)です。乾御門は実際に御所の北西にあるし,「わが庵は都の巽しかぞ棲む・・・」という『百人一首』の喜撰法師の歌は都の東南である宇治に住んでいることを表しています。地球面で北極南極を結ぶ線また天球面上で天頂天の北極南極を結ぶ線を「子午線」と言っています。また時刻表記にも使われ,丑の刻とは1時から3時までの2時間です。それを丑の一刻,丑の二刻,丑の三刻(丑の正刻),丑の四刻と分けるので「丑三つ時」とは2時ころです。ただし時刻ではなく2時から2時半までの時間という説もあるそうです。午前,正午,午後は言うまでもなく午の正刻を基準にしています。十二獣は国によって多少違っています。特に多くに国で亥は豚だそうです。
十干は五行説に由来し,5元素,木(もく,き)・火(か,ひ)・土(と,つち)・金(こん,か)・水(すい,みず)を兄(え)と弟(と)に分けて10種としました。
「甲(きのえ)」は「木の兄」,「乙(きのと)」は「木の弟」のことです。現在ではものの階級・等級・種類・成績を示すとき,また契約書などにおける両者の名称として使われています。優劣がつけにくい時「甲乙つけがたい」という慣用句がありますね。
二十四節気と七十二候
| 季節 | 二十四節気 | |||||||
|---|---|---|---|---|---|---|---|---|
| 気節 | No. | 名稱 | 讀み | 日取り(頃) | 黄經 | 説明 | ||
| 春 | 初春 | 正月節 | 1 | 立春 | りつしゆん | 2月4日 | 315 | 始めて春の氣配が現れて來る |
| 正月中 | 2 | 雨水 | うすい | 2月19日 | 330 | 雪や氷が融け,雨となつて降り注ぐ | ||
| 仲春 | 二月節 | 3 | 啓蟄 | けいちつ | 3月6日 | 345 | 地中に潜んでゐた蟲がはひ出て來る | |
| 二月中 | 4 | 春分 | しゆんぶん | 3月21日 | 0 | 春の中間の日 | ||
| 晩春 | 三月節 | 5 | 清明 | せいめい | 4月5日 | 15 | 櫻等草木の花が咲き始め,萬物に清朗の氣が溢れて來る | |
| 三月中 | 6 | 穀雨 | こくう | 4月20日 | 30 | 春の温かい雨が降つて穀類の芽が伸びて來る | ||
| 夏 | 初夏 | 四月節 | 7 | 立夏 | りつか | 5月5日 | 45 | 始めて夏の氣配が現れて來る |
| 四月中 | 8 | 小満 | せうまん | 5月21日 | 60 | 萬物が次第に成長して一定の大きさに逹して來る | ||
| 仲夏 | 五月節 | 9 | 芒種 | ばうしゆ | 6月6日 | 75 | 稻や麥等芒[のぎ]ある穀物の種蒔きの時期 | |
| 五月中 | 70 | 夏至 | げし | 6月21日 | 90 | 夏の中間の日 | ||
| 晩夏 | 六月節 | 11 | 小暑 | せうしよ | 7月7日 | 105 | 梅雨が明け本格的な暑さが始まる | |
| 六月中 | 12 | 大暑 | たいしよ | 7月23日 | 120 | 暑氣が至り一年で最も暑くなる | ||
| 秋 | 初秋 | 七月節 | 13 | 立秋 | りつしう | 8月7日 | 135 | 始めて秋の氣配が現れて來る |
| 七月中 | 14 | 處暑 | しよしよ | 8月23日 | 150 | 暑さが峠を越えて後退し始める | ||
| 仲秋 | 八月節 | 15 | 白露 | はくろ | 9月8日 | 165 | 大氣が冷えて來て露が出來始める | |
| 八月中 | 16 | 秋分 | しうぶん | 9月23日 | 180 | 秋の中間の日 | ||
| 晩秋 | 九月節 | 17 | 寒露 | かんろ | 10月8日 | 195 | 露が冷氣によつて凍りさうになる | |
| 九月中 | 18 | 霜降 | さうかう | 10月23日 | 210 | 露が冷氣によつて霜となつて降り始める | ||
| 冬 | 初冬 | 十月節 | 29 | 立冬 | りつとう | 11月7日 | 225 | 始めて冬の氣配が現れて來る |
| 十月中 | 20 | 小雪 | せうせつ | 11月22日 | 240 | 僅かながら雪が降り始める | ||
| 仲冬 | 十一月節 | 21 | 大雪 | たいせつ | 12月7日 | 255 | 雪が激しく降り始める | |
| 十一月中 | 22 | 冬至 | とうじ | 12月22日 | 270 | 冬の中間の日 | ||
| 晩冬 | 十二月節 | 23 | 小寒 | せうかん | 1月5日 | 285 | 本格的な寒さが始まる | |
| 十二月中 | 24 | 大寒 | だいかん | 1月20日 | 300 | 寒さが最も嚴しくなる | ||
暦を見ると年間ほぼ15日置きに季節感溢れる名前がついた「二十四節気」というものが目につきます(表6。「清明」とは清らかに晴れ渡った天空と百花が咲き競う大地を満喫できる4月5日ころ,また「霜降」とは北国や山間部では,霜が降りて朝には草木が白く化粧し始める10月23日ころです。二十四節気は中国で太陽の運行に基づいて作られ,太陰太陽暦と併用されてきました。もっとも最近は温暖化のせいで,「小雪」「大雪」など時節に合わなくなったものもあります。図7のA,B,C,Dはそれぞれ春分・夏至・秋分・冬至における地球の位置を表します。地球・太陽・春分点(A)のなす角度を左回り(反時計)に測ったものが太陽黄経λです。二十四節気のうちλが90の倍数になるものが春分,夏至,秋分,冬至で二分二至と言われます。二分二至の中間に立夏立秋立冬立春があり,その前日を節分と言います。現在では立春の前日を指すようになっていますが,本来は1年に4回節分があるのです。λが30の倍数になるものは中,そうでないものは節といわれます。中は旧暦の月の名前を決定するために用いられ,春分は「二月中」で,春分直前の新月の時刻を含む日が旧二月一日となります。また処暑は「七月中」でその直前の新月の時刻を含む日が旧七月一日,その日から数えて7日目が旧七月七日,すなわち伝統的七夕の日です。二十四節気の他に,「入梅はλ=80となる瞬間を含む日」と,また「夏の土用とはλ=117の点を通過する瞬間含む日から立秋(λ=135)前日まで」とλで決められています。
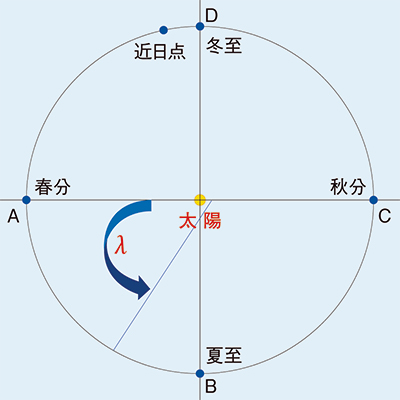
図7 太陽黄経
地球は太陽を焦点とする楕円上を公転運動していますが,その速度は一定ではなく毎年1月5日ころ近日点(太陽から0.9833270AU)を,また7月4日ころ遠日点(1.0166973AU)を通過します。二十四節気の間隔も一定ではありません。その日は毎年±2日の範囲で変わり,実際に計算するにはλを表す式が必要です。太陽は365.2422日で天球上を360度移動しますから1日については平均365.2422/360=0.985647332度,したがって春分からt日後のλはλ=0.985647332・tとなりそうですがもっと複雑です。海上保安庁発行の『天体位置表』にtの3次とsin,cosを含む式が載っており,春分からの経過日数tを求めるためにはこの非線形方程式を解かねばなりません。表7は21世紀になってからの二分二至の日付です。二十四節気は古代中国で発案されわが国でも古くから使われてきました。そのためよく旧暦の用語と誤解されますが,実は地球の公転運動から算出されるものなのです。
お彼岸
昔から「暑さ寒さも彼岸まで」といわれて,秋分のころには夏の暑さも和らぎ秋の訪れを感じるころになりますが,秋分の日とはどういう日なのか案外知られていないようです。
春分・秋分の日には
- ①昼と夜の長さが同じになる。
- ②太陽は真東から昇り,真西に沈む
- ③春分秋分の日の決定は国立天文台で行われる
厳密にはこれらはすべて間違いです。
| 年 | 春分 | 夏至 | 秋分 | 冬至 |
|---|---|---|---|---|
| 2001 | 3月20日(火) | 6月21日(木) | 9月23日(日) | 12月22日(土) |
| 2002 | 3月21日(木) | 6月21日(金) | 9月23日(月) | 12月22日(日) |
| 2003 | 3月21日(金) | 6月22日(日) | 9月23日(火) | 12月22日(月) |
| 2004 | 3月20日(土) | 6月21日(月) | 9月23日(木) | 12月21日(火) |
| 2005 | 3月20日(日) | 6月21日(火) | 9月23日(金) | 12月22日(木) |
| 2006 | 3月21日(火) | 6月21日(水) | 9月23日(土) | 12月22日(金) |
| 2007 | 3月21日(水) | 6月22日(金) | 9月23日(日) | 12月22日(土) |
| 2008 | 3月20日(木) | 6月21日(土) | 9月23日(火) | 12月21日(日) |
| 2009 | 3月20日(金) | 6月21日(日) | 9月23日(水) | 12月22日(火) |
| 2010 | 3月21日(日) | 6月21日(月) | 9月23日(木) | 12月22日(水) |
| 2011 | 3月21日(月) | 6月22日(水) | 9月23日(金) | 12月22日(木) |
| 2012 | 3月20日(火) | 6月21日(木) | 9月22日(土) | 12月21日(金) |
| 2013 | 3月20日(水) | 6月21日(金) | 9月23日(月) | 12月22日(日) |
| 2014 | 3月21日(金) | 6月21日(土) | 9月23日(火) | 12月22日(月) |
| 2015 | 3月21日(土) | 6月22日(月) | 9月23日(水) | 12月22日(火) |
| 2016 | 3月20日(日) | 6月21日(火) | 9月22日(木) | 12月21日(水) |
| 2017 | 3月20日(月) | 6月21日(水) | 9月23日(土) | 12月22日(金) |
| 2018 | 3月21日(水) | 6月21日(木) | 9月23日(日) | 12月22日(土) |
| 2019 | 3月21日(木) | 6月22日(土) | 9月23日(月) | 12月22日(日) |
| 2020 | 3月20日(金) | 6月21日(日) | 9月22日(火) | 12月21日(月) |
| 2021 | 3月20日(金) | 6月21日(日) | 9月23日(火) | 12月22日(月) |
| 2022 | 3月21日(金) | 6月21日(日) | 9月23日(火) | 12月22日(月) |
| 2023 | 3月21日(金) | 6月22日(日) | 9月23日(火) | 12月22日(月) |
| 2024 | 3月20日(金) | 6月21日(日) | 9月22日(火) | 12月21日(月) |
この原因は日の出入りの定義にあります。日の出入りを太陽の中心でなく上辺で定義することで,太陽の半径分だけ日の出は早く,日の入りは遅くなります(太陽の視半径は約15′~時間にして約1分)。
さらに,大気の影響により地平線が浮き上がって見える効果=地平大気差によって,日の出は早く,日の入りは遅くなります(地平大気差は約35′~時間にして2分強)。これらを合計すると,日本付近では太陽は斜めに昇ってくるので約4分の違いになります。日の出で約4分,日の入りで約4分昼が長くなりますから,合計8分ほど昼間が長い,つまり昼間は12時間8分となるわけです。同じ理由で,日の出入り方位は真東や真西ではなくなります。
実際太陽の中心や下端が地平線という瞬間の時刻を測ることは不可能に近いです。また地球大気の屈折のため,太陽に限らず地平線辺りのものは浮き上がって見えます。したがって地平線下の太陽でも見ることができるわけです。日の出日の入り時刻・方位は次のサイトで求まります。 http://eco.mtk.nao.ac.jp/cgi-bin/koyomi/koyomix.cgi
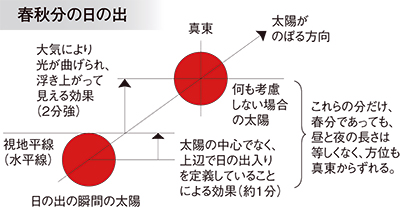
図8 日の出
2017年の秋分の日に,京都で日の出,日の入り時刻はそれぞれ5:45,17:53で昼間の時間は12時間8分で,昼夜の時間が同じになるのは4日後です。また方位はそれぞれ89.4° 270.3°で没入ともやや北よりになります。この値が90° 270°に最も近いのは翌日になります。
では春分の日・秋分の日はどうやって決められているのでしょうか?太陽が天球を1年で1周する間に,春分点を通過する(λ=0)のは一瞬で,その瞬間を含む日が春分日であり,秋分点を通過する(λ=180)瞬間を含む日が秋分日です。その日付は表7の通りで,春分日は閏年とその翌年では20日です。また秋分日は1980年以降は23日でしたが,固定されているわけではありません。2012年以降暫くは閏年では22日になります。
春分の日・秋分の日は国立天文台が算出した結果に基づいて閣議で決定され,それが官報によって告示されて決まります。春分日・秋分日は予め計算できますが,春分の日・秋分の日は前年にならないとわかりません。また春分日,秋分日において日の出・日の入りの時刻は場所によって異なります。東ほど時刻は早まるのは容易にわかりますが,方位は変わりません。
国立天文台暦計算室のページhttp://eco.mtk.nao.ac.jp/koyomi/によると日の出日の入りの時刻方位は(表8)。
同様に夏至とは太陽が夏至点を通過する瞬間を含む日で,この瞬間太陽は最も北に位置し,したがって太陽高度は最高で,影は最短になります。昼間の時間は夏至の前後数日は変わりません。また日の出が最も早い日は夏至の1週間前あたり,最も日の入りの遅い日は夏至の1週間後あたりです。冬至についても同じようなことが言えます。最近では閏年の前年で22日で平年は21日,また冬至は閏年では21日で平年は22日です。詳しい日時は国立天文台暦計算室のページをご覧ください。
| 年月日 (2017年) | 出 | 方位[°′] | 南中 | 高度[°′] | 入り | 方位[°′] |
|---|---|---|---|---|---|---|
| 9/18 | 5:42 | 87 03 | 11:51:11 | 56 49 29 | 18:00 | 272 43 |
| 9/19 | 5:42 | 87 31 | 11:50:50 | 56 26 15 | 17:59 | 272 14 |
| 9/20 | 5:43 | 88 00 | 11:50:29 | 56 02 59 | 17:57 | 271 46 |
| 9/21 | 5:44 | 88 28 | 11:50:08 | 55 39 41 | 17:56 | 271 17 |
| 9/22 | 5:45 | 88 57 | 11:49:47 | 55 16 21 | 17:54 | 270 49 |
| 9/23 | 5:45 | 89 25 | 11:49:26 | 54 53 01 | 17:53 | 270 20 |
| 9/24 | 5:46 | 89 54 | 11:49:05 | 54 29 40 | 17:51 | 269 52 |
| 9/25 | 5:47 | 90 22 | 11:48:44 | 54 06 19 | 17:50 | 269 23 |
| 9/26 | 5:48 | 90 51 | 11:48:23 | 53 42 57 | 17:49 | 268 55 |
| 9/27 | 5:48 | 91 19 | 11:48:03 | 53 19 36 | 17:47 | 268 26 |
緯度:35.0167° 経度:135.7500° 標高: 0.0m 標準時:UT+9h ΔT=68s
「彼岸」とは春分の日・秋分の日を中日として前3日・後3日の計7日間を指しますが,元来はあちら(彼方)の岸,すなわち煩悩のない,涅槃の世界という仏教用語です。亡くなった先祖たちの霊は「彼岸」に住んでいるということから,「彼岸に墓参り」と言う習慣ができました。春秋の先祖供養は西方浄土と結びつけて説明される場合が多いですが,上記のことをまとめて考えてみると,仏教の行事というより太陽信仰時代からの習慣のようにも思えます。
なお「国民の祝日に関する法律」には春分の日は「自然をたたえ,生物をいつくしむ」,秋分の日は「祖先をうやまい,無くなった人々をしのぶ」と書かれています。
七十二候
二十四節気をさらに3分割して季節の名前を付けたもので,古風な漢字3文字または4文字で表されます。古代中国で作られ何回か名前は改定されているそうで,現在の呼称は明治になってからです。
太陽黄経5°刻みすなわちほぼ5日づつの季節の言葉を綴った暦で,いかにも東アジア農耕民族の特徴を表しています。玄鳥至とはつばめが南国から渡って来る清明の初候4月初旬のころで,玄鳥去とは南国へ帰っていく秋分の少し前9月中旬のころですが,最近つばめは見かけなくなりました。蚕起食桑(5月20日ころ)や麦秋至(5月末)といっても養蚕や麦作はほとんど見られなくなりました。
暦計算のウェブサイト
筆者のページでhttp://web1.kcg.edu/~sakka/koyomi/eto.htm
任意の日の曜日,干支,MJD,太陽黄経が求まります。

図9 干支・曜日・太陽黄経を算出するページ
最初のテキストボックスには予め入力した年月日とその年の干支と二分二至が自動的に表示され,[計算]ボタンをクリックするとその日のMJD,基準日からの日数,太陽黄経,曜日,干支が表示されます。別の日付を入力して計算ボタンをクリックするとその日の諸量が表示されます。間違って6月31日と入力しても自動的に7月1日に変換してくれます。
MJD(修正ユリウス日)とは1857年11月17日世界時0時0分からの通日で天文学ではよく使われます。太陽黄経はその日の日本標準時9:00(世界時0:00)における値で,1年で360°進むから1日につき0.985646523°進む。逆に0.1°進むには約2時間半となります。
入力する年月日はグレゴリオ暦値であり,1582年10月15日以降有効です。それより前はユリウス暦値に次のxを加えてグレゴリオ暦値に変換する必要があります。
x=s-[(s-1)/4]-z ただしs(≠0)は世紀値で,zは3(s>0)または2(s<0)。日付の世紀数を入力し変換ボタンをクリックすれば,xが計算され後のテキストボックスに表2の値が表示されます。
- ◆例1 殷と周の最終戦,牧野の戦いの日であるBC1046年1月20日をグレゴリオ暦値に変換すると-1045年1月10日となり,この日付で干支を求めると甲子となり『史記』の記載通りです。
- ◆例2 『御堂関白記』に藤原道長と安倍晴明が宇治木幡に行ったのは長保六年二月十九日,癸酉の日曜日と記してます。これを西暦に変換してみよう。この年は1004年であり3月においてこの干支になる日を順に探していくと18日が求まります。干支と曜日が一致するのは420日(60と7の最小公倍数)周期だから1004年にはこの日しかないです。ただし,これはグレゴリオ暦値だからユリウス暦の日付にすると,11世紀だから差は6日で3月12日となります。
- ◆例3 夏の土用は太陽黄経が117°になる日から135°になる前日までの期間です。2018年の土用丑の日を求めよう。 7月20日9時の太陽黄経は117.27°で117°になるのは約7時間前だからこの日が土用の入りです。8月7日9時の太陽黄経は134.47°でこの日のうちには135°を越えるので6日までが土用です。 この期間に丑の日は7月20日(金)と8月1日(水)の2回あります。
- ●国立天文台暦計算室のページ http://eco.mtk.nao.ac.jp/koyomi/
- 日の出入・月の出入・月齢・二十四節気・日月食予報などほとんどの主な天文現象が計算できます。ただし1960〜のみ。
- ●こよみのページ http://koyomi8.com/
- 万年カレンダー・二十四節気・七十二候・日の出入・月の出入・月齢・日月食予報さらに和暦西暦変換・花暦などほとんどの天文暦計算ができます。
- ●和暦のページ http://www.wagoyomi.info/
- 旧暦と現行暦の曜日・干支・二十四節気を含む変換ができます。
- ●図1 ユリウス・カエサル https://ja.wikipedia.org/wiki/%E3%82%AC%E3%82%A4%E3%82%A6%E3%82%B9%E3%83%BB%E3%83%A6%E3%83%AA%E3%82%A6%E3%82%B9%E3%83%BB%E3%82%AB%E3%82%A8%E3%82%B5%E3%83%AB
- ●図2 ウマル・ハイヤーム https://ja.wikipedia.org/wiki/%E3%82%A6%E3%83%9E%E3%83%AB%E3%83%BB%E3%83%8F%E3%82%A4%E3%83%A4%E3%83%BC%E3%83%A0
- ●図8 日の出 http://eco.mtk.nao.ac.jp/koyomi/wiki/C6FCA4CEBDD0C6FEA4EAA4C8C6EEC3E62FC3EBA4C8CCEBA4CEC5F9A4B7A4A4C6FC.html



