Accumu Vol.24

ディジタル情報の多様性を支える原理

元京都情報大学院大学教授山縣敬一

京都大学工学士，同大学院博士課程満期退学（数理工学専攻），工学博士（大阪大学）。広島大学名誉教授，元社団法人情報処理学会中国支部長。京都情報大学院大学開学時の2004年4月から教授に就かれ，2016年3月まで務めた。「計算機システム特論」や「生産システム工学特論」などの講義を担当されたほか，京都コンピュータ学院でも計算機アーキテクチャ，数値解析などの授業を受け持たれた。2016年3月28日にはKCG京都駅前校で退職記念講演会に臨まれた。

1はじめに

人間は，自然界にあって太陽エネルギーの恩恵を受け，畑を耕し，狩猟をし，漁をすることで生活してきた。その環境にあって，人は，視覚，聴覚，触覚，味覚等々のセンサーによって自然界から多様な情報を受け取っていた。また一方において，文字，数字，記号，数式などといった人工的な記述された情報の社会を構成するようになった。単なる話し言葉だけでなく，これらを記述できるようにしたのは，人間だけである。人間の自然界での世界と，文字や記号で記述された世界は，お互いに対応がとれるけれどまったく同じではない。最近の僅か50年ほどの間に，コンピュータが発達し，情報ネットワークが世界中に張り巡らされ，記述された情報（ディジタル情報）が地球全体を覆うWWWに流れており，データ自体が多様な社会活動の資源となっている。筆者がここで考えたいことは，自然界にいる人間がこのディジタル情報を有効に利用するための原理をつかんでおきたいということ。そのために，すでに分かっていることではあるがC.E.シャノン（1916〜2001）の情報通信の考え方と，J.B.Jフーリエ（1760〜1830）のフーリエ変換の意味をもう一度理解しておきたいというのが，この小文の目的である。

2アナログ情報のディジタル化

1960年代，コンピュータが世の中全般に普及し，コンピュータは広義の意味での計算に多大な能力を発揮するようになった。1980年代にはUNIXを基礎とするコンピュータネットワークが構成されて活用されるようになる。その当初は，文字や記号で表されたディジタル情報が主であった。しかし，この時代になるとそれまでアナログ情報として扱われていた物のディジタル情報への変換が急速に進む。もちろん，この技術が急に現れたわけではなくて，記録の信頼性の意味から以前からパルス符号化による記録の研究は行われていたと思われるが，実際のわれわれの生活に密着して使われるようになったのがこの時期である。

コンサートホールでは，放送局が磁気テープに演奏を録音し，記録として残して放送にも利用した。また，われわれもフィルムカメラで写真を記録として残した。人の本来の在り方からすれば，音楽はコンサートホールで生演奏を聴き，写真も自分の肉眼で見たもので満足していればよいが，やはり特に写真のような場合は記録を残したくなる。しかも現在では，情報の記録を残すだけでなく，それを通信に使うことが不可欠になった。音楽の磁気テープ録音やアナログのLPは，あくまで音の空気振動をそのまま忠実に記録したもので，ディジタル情報にはなっていない。アナログ情報でもある程度の編集はできるし，不特定多数向けの放送には使える。しかし，電話のように情報の記録よりも通信が主体になると，ディジタル化の効果が大きくなる。昔の固定電話は音声を電気信号にかえて電話線を通じて相手と情報交換を行った。この場合，記録はどこにも残らない。しかし，話す相手は固定されていないから，番号をダイヤルすることで，交換機のスイッチを切り替えた。この場合のスイッチは完全に機械的なスイッチで電話線をつなぎかえるもの。これが，1980年ごろに音声がディジタル化されパルス符号になったことによって，機械的スイッチはすべてメモリを使った電子回路による切り替えに変わった。

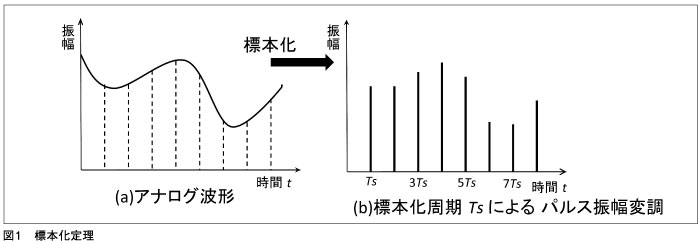
文字や記号のようにもともと離散的なデータの場合，コンピュータの状況に合わせて0と1で2元符号化すればディジタル情報になる。音声や画像のようにもともと自然界から取り込んだものは，例えば音声なら時間とともに連続的に変化する空気振動の波であって，そのままでは0と1で符号化できない。これを離散的な値に分割する必要があるが，そこに使われるのが，標本化定理である［2］。

1928年にナイキストが発見した定理で，当然この時代にコンピュータでのディジタル処理の考え方はなかったはずで，現在の情報のディジタル表現にこれを利用したのは，シャノン（1916－2001）による再発見と言われている［3］。この条件の下では，以下の図のように，連続的に変化する波形を標本化周期で離散的な振幅の列に変換できる。理論上は，標本化にインパルス応答を適用するので，現実にAD（Analog to Digital）変換をすれば，誤差を伴うのはやむをえないが，理論上は離散化しても情報が失われることなく，元の波形が復元できることになる。ここで証明はできないが，標本化周波数が非常に重要で，これは次に述べるフーリエ変換が背景にあって，時間的に変動する波形があったとき，これは表現を変えるといろいろな周波数の三角関数に分解できことを利用している。

実際の応用では，それぞれの場合に応じて標本化周期を決めるが，CDの場合は人間の聴覚が聞き取れる音の周波数20kHzを考慮して，44.1kHzで標本化を行い［5］，最初にディジタル化の行われた家庭の固定電話では，人が自然に話をするときの音域4kHzを考慮して，8kHzで標本化している。標本化した後振幅の列が得られるが，これを何ビットで2元符号化するかは，音の大きさ（ダイナミックレンジ）の範囲内で小さな音をどこまで聞き取りやすくするかで決めている。CDでは16ビット, 固定電話では8ビットである。ただし, モバイル機器については使い道と機種によって異なっている。いずれにしろ, 結果的に表面上は0と1の2元符号で表現されるが，情報として持っている性質は文字や記号とは全く異なったものになっている。

3フーリエ級数とフーリエ変換

フーリエ変換の理論そのものをここで解説はできないので，前節に取り上げた音声の場合，ディジタル化するのに元の音源の周波数と標本化の周期を対応させて使っている。これは，現在ではよく知られていることであるが，音声はいろいろな周波数の波の重ね合わせで成り立っている。ある音源が与えられると，そこに含まれている周波数成分によって，音の性質を調べることができる。そして，一つの周波数の波は三角関数で表されるので，これを三角関数の級数展開で表すことができる。これをフーリエ級数で表すと次のようになる。ここで周期T（角周波数ω）をもつ周期関数のフーリエ級数展開は次式で与えられる。

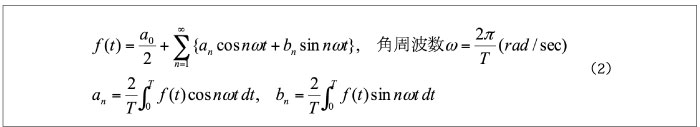
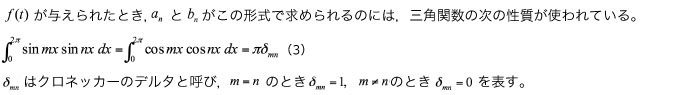
この（3）式の性質は，三角関数が直交関数列になることを表していて，この性質の恩恵によって，多くの周波数成分の和の中から特定の周波数の成分を取り出すことができる。フーリエ変換の一般形はこの後すぐ述べるが，もともとフーリエ（1760-1830）がフーリエ級数展開を考えたのは熱伝導の微分方程式を解くためであった。連続体力学においては，変動する未知関数を直交関数展開で表現してその性質を調べることがよく行われる。連続体の振動問題でも境界値問題がフーリエの方法で議論されるが，ここではこの問題にはこれ以上立ち入らない［6］。

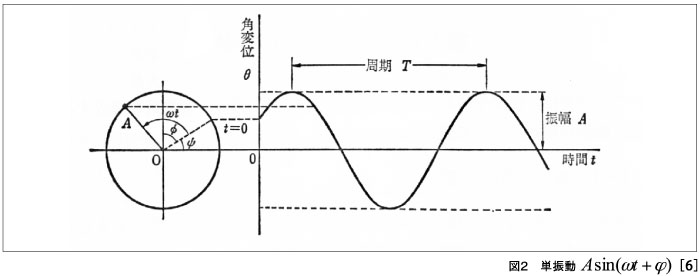
ここでは，音声を応用対象として考えているので，一つの三角関数は図2のように時間を変数とした単振動の表現になる。この波形は時間的にいくらでも長い間隔を考えられるが，この一つの関数を決めているのは，振動数（周波数）と振幅と位相（ψ）の僅か三つのパラメータだけで無限の波形が定義できている。ここで，位相は基準の時刻例えばt＝0における偏角を表していて，これによって全体の位置がきまる。このためにsin関数とcos関数の両方が使われている。（2）式のフーリエ級数は，この単純な波形のパラメータが少しずつ違うものを集めることで任意の音声が表現できることを示している。ここで計算については述べないが，非周期関数も扱えるように周期Tを無限大まで広げ，次のオイラーの公式を使って，三角関数を指数関数の複素数表示に書き換えると，表現が簡潔になる［1］。

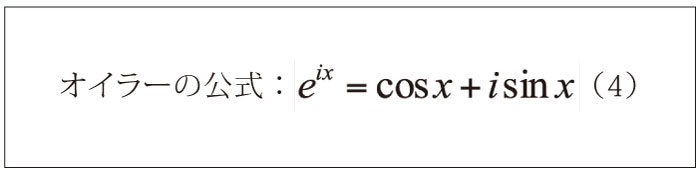
式（2）において，Tを無限に大きくすると，ωは限りなく小さくなる。もともとフーリエ級数は角周波数ωの異なる三角関数の和になっているが，Tを限りなく大きくして非周期関数も扱えるようにした場合，これはωについての積分に表現される。この結果，フーリエ変換並びにフーリエ逆変換は（5）式のようになる。

異なった形式に見えるが，これが（2）式のフーリエ級数を非周期関数まで広げて，三角関数を複素数表示にしたものである。（5-1）は音声で言えば時間的変化の関数で，（5-2）は角周波数の関数で相互に変換が可能になる。その意味で，（5-1）はフーリエ逆変換と呼ばれる。これらは，理論上の関係式だが，フーリエ変換についてはFFT（高速フーリエ変換）の数値解法が分かっておりプログラムが用意されている。

理論の解説が長くなってしまったが，ディジタル情報のメディア処理に話題をもどすと，例えば音声のデータは，時間による音の変化と考えてもよいし，周波数ごとの音の集まりと考えてもよく，どちらの表現を使っても，同じ内容を表していることになる。そこで，人の聴覚特性から考えると周波数の成分が関わるため，前節の標本化定理がなりたち，直感的には時間的に切ってしまっても，聴覚で感じ取れる周波数の音声は復元できることになる。さらに，現在のメディア処理における音声は，単純に標本化を行うだけではなく，いろいろな目的に応じて多様な処理を行って，ネット上に流れ，コンピュータのメモリに蓄積されている。その種類は非常に多く筆者もすべてを説明できないが，音楽の場合，MP3プレイヤーでは，CDの場合の約1/10のデータ量で人の聴覚で十分満足できる音楽を聞かせる。これは，周波数だけの処理ではないが，人の聴覚と音楽の音の変化の特性により，人の聴覚に敏感な部分には十分なビット数を割り当て，聴覚であまり敏感でないところでは，情報量を減らしている。単純な説明であるが，これが情報圧縮と呼ばれていることの，もっとも基礎の部分である。また，逆に標本化定理を効果的に使って，従来のCDの音声に満足しない人向けに，敢えて標本化周波数を96kHzや192kHzにあげ，量子化ビット数を1サンプル当たり24ビットあるいは32ビットとするハイレゾ音源（高分解能の音源）がネット上に配信され，それに対応する音響機器が普及して，経済効果を生んでいる。

音声データが，時間の関数としてみても，周波数の関数としてみても同じ情報であることは，いろいろなところで応用されている。このフーリエの考え方は，もともとアナログ情報での議論であるが，これがディジタル化されたときにも活きていることが重要である。音声でいえば音の周波数と人の聴覚が密接に関係しており，ディジタル化されて必要に応じて情報量（ビット数）の増減を図るときにも，単純にビット数を減らすのでなく，人の聴覚を考慮し，そして用途に応じて無駄のないよう合理的な情報量が定められている。

4画像における空間周波数

これまで，主に音声のディジタル化とメディア処理について述べてきたが，その他のディジタルメディア処理についても，対象によってこれまでの原理の応用の仕方に違いはあるが，大部分の考え方にフーリエの周波数の分布を利用することが用いられている。身近な例で，フィルムカメラのアナログ画像からディジタルカメラによる画像のディジタル化を要点のみ述べる。ディジタルカメラでは，撮像素子で画像を取り込むときに情報量が決まる。画像の場合，精細な画像であるほど多くの画素数になるので，フルカラーの場合の情報量が多量になり，目的に応じた画質の情報量の管理が問題になる。画像は静止画だけでなく，ビデオに始まってテレビがハイビジョンのディジタルになり，4Kテレビまで具体化してきて動画一般の扱いが圧縮の規格なしでは成り立たなくなっており，MPEGの規格が応用対象に応じて何種類も定められている。

ここでは，画像処理圧縮の一番基礎になっているJPEGについて，原理のみを説明する。JPEGは普段ディジタルカメラの静止画の保存や伝送に最もよく使われている規格である。実は，この圧縮原理も音声の圧縮と根本のところは同じ原理でフーリエ変換を使っている。静止画には時間による変化はないが，例えば横方向の1本のスキャンラインに沿って，赤色の明るさの変化を見れば，スキャンラインに沿う波形が得られる。これのフーリエ変換を求めれば，明るさの変化の周波数成分が得られる。これを空間周波数と呼び，実際には2次元に展開して平面上の明るさの変化を見る。人の視覚の特性として，空間周波数の高いところは細かく模様が変化するところで，人の目あまり細かい変化はよく見ていないので，ビット数を減らしても実用上問題はない。一方，空間周波数が低いかあるいはほとんど0になって変化がない場合，同じ色調が続くことになるが，この部分の色調は人の目は敏感である。よく言われることだが，洋服や着物の色合いを見る人の目は非常に敏感であると言われている。この部分は多くのビットを割り当てて，微妙な色合いを区別する。このほか，同じ色の画素が並ぶところは，そのまま同じビットパターンを繰り返すのではなく，そのパターンが幾つ続くかのデータで置き換える（ランレングス符号化）。細かい技術はいろいろ使われているが，人の目の感覚に合わせるのには，元の画素の並びよりも空間周波数で変化の仕方を見る方が効果的である。音声であれ，画像であれ，最後に人がその情報を受け取るときには，アナログ情報として受け取る。従って，ディジタル化したときにその特徴が失われないようにすることが大切である［2］。

5機械制御における計測

CDやディジタルカメラの普及で，パソコンの身近な応用として各家庭にディジタル機器が使われるようになった。しかし，もともとディジタル技術は古くから技術的には研究されていた。話題が変わるが今後ますますインターネットに流れるディジタル情報は多様化しつつあるので，筆者の一つの経験に過ぎないが1例を挙げる。機械制御において，工作機械（筆者が実際に使ったのはフライス盤）で工作物を固定したテーブルや切削工具を付けたヘッドを仕上がり形状に合わせて移動させるために，基本的に数値制御と言って数値データで移動の寸法を動かす。これが普及し始めるのが，ディジタル回路が使われるようになった1950年代。これで，コンピュータによる制御が可能になるが，やはり数値データだけで制御はできない。工作機械が数値データを受けて工具とテーブルを動かしても，現実の物理現象には誤差が入り込む。潤滑油の摩擦による位置決め誤差，工具にかかる力とたわみ，工具摩耗による誤差，時間の経過による温度上昇と熱変形，かかる力による振動現象，など。このような誤差要因も計測して補正をかける。これらのデータの中にはアナログ情報も多いため，コンピュータで処理するためにはADコンバーター（Analog to Digital）を利用し，ディジタル情報にしてコンピュータで処理し，生産システム内に張り巡らされたネットワークで別の行程と連携をとる。データのサンプリング（標本化）の原理は同じであるが，このような状況では，数値というディジタルデータと計測によってアナログ情報から得られるデータの共同作業で仕事が進む。

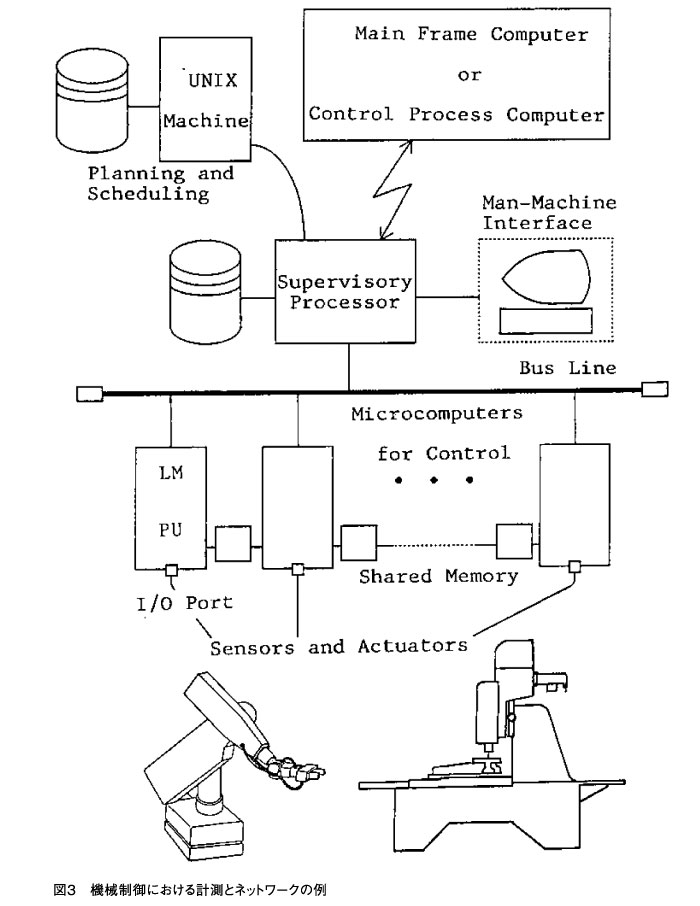
参考のために図3は，筆者が1970年代に基礎実験に利用していたシステムで小規模のことしかやっていないが，現在ではこのようなシステムが大規模なネットワークに接続されて，コンピュータの間でのデータ交換で作業が進められる。

そして，次第に具体的な話題が多くなってきたIoT（Internet of Things）では，家電機器から製造現場に至るまでいたるところで計測が行われ，アナログ情報もディジタル情報に変換されて，地球上のグローバルなネットワークに流れることになる。IoTにおけるThingsには何の規定もないので，ありとあらゆる情報が利用され，しかも情報は，人に送られるというよりは，機器同士あるいはロボットを受信者とする複雑なネットワークになる。そしてこの複雑なネットワークの全体が一つのシステムとして機能し，人の生活に役立つものでなければならない。そこでは，どこかで発生した故障が，極力小さな範囲で抑えられ，全体に波及することを避けなければならない。どのような状況にあっても，人の生活に悪影響を及ぼすようなことがあってはならず，常にシステム全体が人の生活に役立っていなければならない。

6おわりに

音声，動画，その他の計測データなど，これまでコンピュータ処理と通信の対象外であったものが，ディジタルデータとして処理が可能となった。ビッグデータと言うまでもなく多量のデータがサイバースペースに流れており，その量も質の多様性も日に日に増加している。電力供給の自由化が実施され，おそらく各家庭の使用電力のメーターはスマートメーターとしてネットワークに接続されるであろう。このような仕組みが次々に増加してサイバースペースにデータが流れ，これが社会を動かしていくことになる。ここからの結論は筆者の主観が強く出てしまうが，いかにサイバースペースが巨大化し，そこでの情報の流れが膨大になっても，本来人のよって立つ自然の世界と同じにはなり得ない。あくまでも，自然のディジタル化されていない世界と巨大なサイバースペースは二重構造をなし，人はこの二つの世界で未来への道を歩むことになる。そのときサイバースペースを人の生活の向上に役立たせるためには，ディジタル情報からなる巨大なサイバースペースの舵取りが必要である。もともとディジタル情報が人の管理のもとで作られるとすれば，それは，可能なはずである。そういえば，ウィーナーのサイバネティクスの著作に，サイバネティクスの語源は，ギリシャ語で「舵をとる人」の意味であると書いてあったことを思い出す［7］。

参考文献

［1］小暮陽三，”なっとくするフーリエ変換“，講談社，2001．
［2］小川英一，”マルチメディア時代の情報理論“，コロナ社，2007．
［3］高岡詠子，”シャノンの情報理論入門“，講談社ブルーバックス，2012．
［4］クロード・E，シャノン，ワレン・ウィーバー，植松友彦訳，”通信の数学的理論“，ちくま学芸文庫，2014．
［5］中島平太郎，小川博司，”図解コンパクトディスク読本（改訂2版）“オーム社，1988．
［6］中川憲治他，”工業振動学第2版“，森北出版（株），1986．
［7］ノーバート・ウィーナー，池原止戈夫他訳，”サイバネティックス第2版“，岩波書店，1962．