Accumu Vol.11

形状情報処理について

イリノイ大学アーバナ・シャンペーン校准教授 品川 嘉久

1 はじめに

我々の身の回りの物（机，コップ，人体…など）は，様々な形をしている。こういった物の「形」をコンピュータで認識し，扱うためには，それを何らかの形で「数値化」する必要がある。では，どのようにして個々の形のもつ特徴を抽出してその情報を数値化すればよいのであろうか。

物の形の持っている情報のことを，本稿では形状情報と呼ぶことにする。そして，物の形状がもつ膨大な形状情報の特徴を，特異点と呼ばれるものの持つ僅かの情報で表し，記述したり認識したりする方法について解説する。また，物の形状を，最初はおおまかにとらえ，次第に細かいところを調べるための方法としては，多重解像度解析という手法を用いる。

2 トポロジー

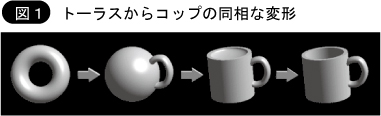
物体の形を表す数学的道具がトポロジー（位相）である。ある形を，ちぎったりくっつけることなく，粘土細工のように，連続変形して，別の形になるとき，それらの形は同じトポロジー（同相）であるという。例えば，コップの表面とドーナッツの表面（トーラスと呼ばれる）は同相である。しかし，球面とトーラスは同相でない。

コップとトーラスの区別がつかないことからもわかるように，このトポロジーだけでは，物体の形状を実用的に表すのに十分でない。そこで，我々は特異点に基づく方法を提案している。

例えば，人間が地形を認識する時のことを考えてみよう。我々は地形を頂上，底点，そして峠といった，特徴を捉えることによって認識する。これらの点は，「特異点」と呼ばれる。別の例をあげよう。エネルギーポテンシャルを考えた場合，それらの特異点は平衡状態を表している。このことからも分るように，物体を特徴付けるのに特異点は非常に重要な役割を果たす。この特異点は数学のモース理論によって，その物体の形状の特徴と密接に関係している。我々は，特異点間のグラフ的関係を与えるレーブグラフ（Reeb graph）を用いる。そして，レーブグラフとモース理論に基づいた物体形状の符合化法〔3〕について述べる。これによって，物体形状を符合として操作することが可能になる。

2.1 特異点

簡単な例として，この局所座標系の上で，高さ関数を定義する。高さ関数は，与えられた点の，高さ（物体が埋め込まれている3次元空間の中での例えばz座標）を返す関数である（注1）。高さ関数h:R2→Rのヤコビ行列は

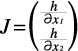
で与えられ，特異点はこれが0ベクトルとなる点である。hの特異点とは，頂上点・鞍点・谷底点である。谷底点と頂上点は，面上で高さ関数hが局所的最小および最大になる点であり，鞍点は，hが一方の方向から見ると極小であり，別の方向から見ると極大になる点である。特異点においては，法線ベクトルは高さ関数と同じ方向を向いている。

（注1）高さでなくてもC²級関数であればよい。例えば，後述するように，画像の輝度，曲率などを用いる応用もある。

次に，高さ関数h:R2→Rのヘッセ行列は

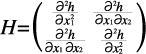
で与えられる。そのヘッセ行列が正則であるような特異点を，非退化であるという。特異点におけるヘッセ行列の負の固有値の数を，その特異点の指数と呼ぶ。頂上を表す特異点は指数2，鞍点は1，谷底は0となる。トーラスの場合，指数2の特異点は1個，指数1の特異点は2個，指数0の特異点は1個となっている。

2.2 レーブグラフ

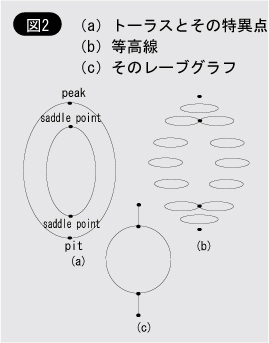
次に，特異点のお互いの関係を，レーブグラフと呼ばれるグラフで表現する（図2）。それは次のように定義される。レーブグラフは，物体表面を等高線で表し，各等高線の連結成分を一つの点として表して得られるグラフである（注2）。

注2）高さ関数でなくてもよい。多様体M上の任意の実関数f:M→Rについて，fのレーブグラフとは，fのグラフM×Rの，(X1, f(X1))～X2, f(X2)) という同値関係による商空間である。ここで，この同値関係～は，f(X1)) = f(X2)) かつ X1,X2が f^-1(f(X1)) と同じ連結成分であるとき成り立つとする。

例えば，図2（a）に示すようなドーナツ型の曲面（トーラス）の等高線は図2（b）のようになり，そのレーブグラフは図2（c）のようになる。

この図からもわかるように，レーブグラフは，その物体の「骨組み」を表す。

このレーブグラフで特に重要なのは，曲面の頂上，鞍点，谷底を表すノードであり，これらの点は高さ関数の特異点そのものである。

3 レーブグラフとモース理論に基づく物体の符合化法

いよいよ，物体の形を「数値・記号」で表すことを考える。形状情報を「数値・記号」で表すことを，以後，符合化と呼ぶ。このとき，先ほどの特異点が役に立つ。モース理論を用いると，大雑把に言えば，物体の形はその特異点の指数と同じ次元を持つ胞体というものを張り合わせて復元できる。簡単に言うと，2次元胞体は椀を伏せたような形，1次元胞体は紐のような形，0次元胞体は一つの点で表すことにする。元の物体の形はそういったものを張り合わせて，粘土細工のように変形して得られる。この変形をホモトピー変形という。トーラスを例にとると，指数2の特異点は1個，指数1の特異点は2個，指数0の特異点は1個あるから，モース理論によると，2次元胞体1個，1次元胞体2個，0次元胞体1個を張り合わせて得られる。

物体形状の符合化はこの胞体およびその張り合わせの順序・位置を記述することによって行なう。具体的には，2次元胞体を張り合わせるput_e2，1次元胞体を張り合わせるput_e1_divideとput_e1_merge，および0次元胞体を張り合わせるput_e0の4種類のオペレータがある。例えば，先ほどのトーラスは，

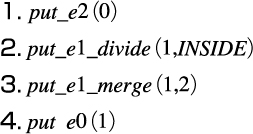
という「数値・記号」（符合）で表される。各オペレータのパラメタに現れる数字は，その高さでの物体の切口の輪郭線に与えられた番号である。

パラメタについての詳しい説明は，[3]に譲る。胞体を張り合わせる順序は，レーブグラフによって示されている。この符合化法により，物体の位相を符合として操作することが可能になる。1次元胞体の張りつけには，次のように4種類に分けられる。

4 ホモトピー変形

任意の断面における等高線間の包含関係は，木構造で表される。物体の上から下へと断面を移動していったとき，この木構造は，特異点を含む断面のみで変化し，その他の断面では変化しない。つまり，ホモトピーによる等高線の連続的変形が可能であり，等高線をホモトピーによって変形する軌跡として物体表面を構築することができる。この方法は，CT画像や標本切片などから物体を再構築することにも応用でき，従来の三角形近似やスプライン近似による歪んだ物体表面が構成されるのを避けることが可能になった（図7）。

その考え方は以下の通りである。二つの隣合った輪郭線の間に張られる物体表面は，一方の輪郭線が他方の輪郭線へホモトピーによって変形される軌跡だと考えるのである。つまり，二つの輪郭線が，媒介変数表示によって各々

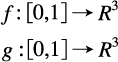
で表されるとき，この両者の間に張られる曲線はfからgへのホモトピーG

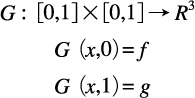
で表される。f,gへの媒介変数の入れ方については，我々は連続的トロイダル・グラフを用いて決める方法を開発した[5]。

このホモトピーを用いたモデルにより，これまでにあった三角形分割を用いる方法とスプライン近似を行う方法の両者を統一し，さらに一般化して表現力を高め，これまで両者が抱えてきた，3次元表面全体における凹凸頂点の情報，峠点の情報を得るための表面全体の一次，二次微分を求めることの困難などの数々の問題点を解決することが可能となった。

5 ホモトピーモデラ

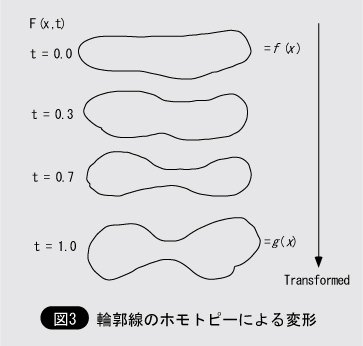
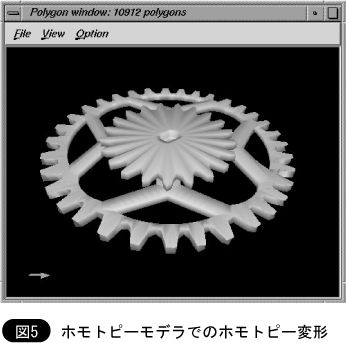
図3に示したような，ホモトピー変形に基づいて，物体形状を作る3次元CADシステムであるホモトピーモデラを構築した。本システムでは，

1，レーブグラフと輪郭線の指定

2，ホモトピー変形の指定

というステップで形状を生成する。レーブグラフは，3次元の線画を描くようなドローイングツールと同様のインタフェースを持つ。ホモトピー変形は，システムが自動的に生成する。これをエディットすることもできる。

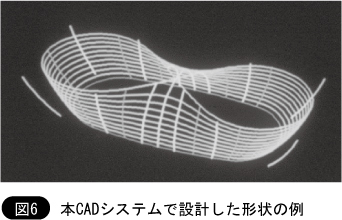
図6は本CADモデラで構築した物体の例である。

6 3次元形状復元への応用

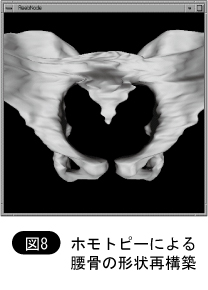
ホモトピーモデラは，CADによる形状設計だけでなく，医用データや，地形の標高データから，形状を作り出すのにも応用できる。医学の分野はコンピュータ・グラフィックスに多大な期待を寄せている。医師が得られる画像は，X線CT，MRIにみられるような2次元の断層画像にしかすぎないため，全体の構造を把握するには，それらを3次元に構成し直さなければならないからである。ホモトピーモデラでは，まず断層画像から輪郭線を抽出し，隣合った輪郭線の間にホモトピーを用いて連続な立体表面を再構成させる。つまり，離散的な2次元情報の集りから連続な3次元情報を復元するのである。離散的な輪郭線からレーブグラフを求める方法は[4]で開発した。

7 地理情報システムへの応用

断層画像からの3次元物体再構築方法は，地形データにも応用できる。我々は，輪郭線ではなく，格子点状にならんだ各測量点での標高データで与えられた地形情報から，正確に特異点を抽出し，レーブ・グラフを構築する方法を開発した [8]。

図9に芦ノ湖周辺の地形データからの情報抽出結果を示す。

8 形状データベースへの応用

3次元形状のレーブグラフによるマッチングを用いれば，3次元形状のデータをデータベースからサーチすることができる。高さ関数は，高さの方向による依存性がある。3次元物体形状を生成・再構成する際にはあまり問題にならないが，データベースから物体をサーチしたり，形状を認識する際には障害となる。そこで，サーチや形状認識のために，測地線に基づく距離関数のレーブグラフを用いる方法を開発した[1]。

例えば，図10（a）に示す物体（車）と似た形状を，数百個のモデルの中から検索して得られたのが図10（b）-（e）である。

9 特異点フィルターに基づく画像のマッチングとホモトピー変形

輪郭線だけでなく，ホモトピーを画像のマッチングや変形に用いることができる。この場合，用いるのは，高さ関数ではなく，画素の輝度関数となる。我々は，与えられた二つの画像を完全に自動的にマッチングする方法を開発した[6]。まず，非線形フィルタによる，各画像の特異点の階層を提案した。このフィルタは，1次元の頂上点を保存するフィルタα，谷底点を保存するフィルタβの2次元テンソル積として，

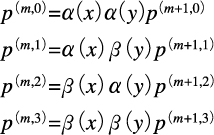
の4種類ある。

ここで，p^（m,i）は，解像度レベルmのフィルタiへの応答である。これらのフィルタは，画像の大きさを1／4に縮小する性質を持つ。

次に，その各階層の間の

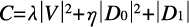
の値を計算し，これを最小化するマッチングを求めている。ここで，Vは輝度値の差，D0は階層間の画素の距離，D1は画像の変形度である。λ，ηの値も最適なものが理論的に自動的に定まる。

既存の方法で，画像のマッチングが困難であった理由は，ウェーブレットなど階層的線形フィルタは，階層上位ほど，輝度と位置の情報を失うためである。前述の非線形な特異点フィルタは，その情報を保存するため，完全な自動マッチングが可能となった。これを用いれば，完全自動モーフィング，動画像圧縮，ステレオ画像からの立体形状復元，モーションキャプチャなどに応用できる。

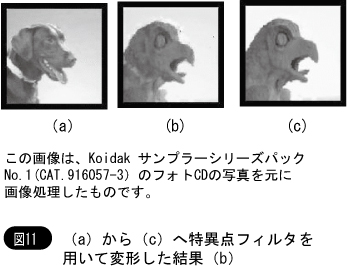
また，2枚のCTの間の補間ができるので，正確なボリュームレンダリングを実現できる。図11にその一例を示す。

10 表情認識への応用

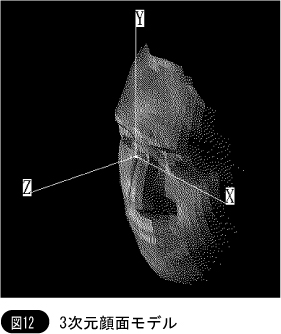
我々は，顔面形状を，特異点を用いて特徴付け，表情を解析する方法を提案した[7]。人間の顔面は感性情報を伝達するための重要な道具の一つであり，工学・医学・人類学・心理学・生理学などの種々の方面からの研究がなされている。特に近年は，セキュリティシステムやマンマシンインターフェースおよび遠隔通信システムなどの応用分野において，ビデオカメラおよび計算機を用いた自動システムの構築が広くなされており，顔の研究の重要性が高まってきている。我々は，顔の形を立体として測定（3次元測定）し，表情の変化を立体の形の変化として捉えた。人間の顔面に現れる詳細な形状を安定に捉えるために，データの入力にはライティングスイッチフォトメトリー法[2]を利用し，顔面上の各点における法線ベクトルを得て，積分により，図12に示すような3次元形状を得る。

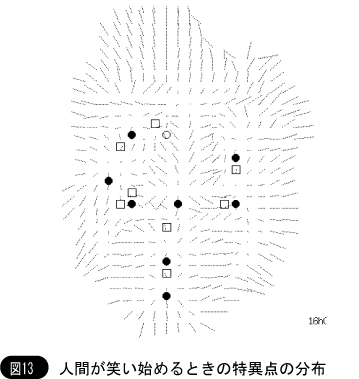
そして，このベクトルを利用して特異点を計算し，また，目・眉・口などの表情の特徴を安定に抽出する。

図13は，笑っている表情の特異点の分布を示す。

11 まとめ

形状情報処理は，まだ若い分野である。本稿によって，この分野に興味をもつ人が少しでも増えれば幸いである。

参考文献

〔1〕M. Hilaga, Y. Shinagawa, T. Komura, and T.L. Kunii. Topology matching for i full automatic similarity estimation of 3d. In Proc.SIGGRAPH 2001, pages 203-212. IEEE Computer Society Press, Los Alamitos, 2001.

〔2〕H. Saji, H. Hioki, Y. Shinagawa, K. Yoshida, and T.L. Kunii. Extraction of 3D shapes from the moving human face using lighting switch photometry. In N.M. Thalmann and D. Thalmann, editors, Computer Animation '92, pages 69-86. Springer-Verlag, 1992.

〔3〕Y. Shinagawa, Y.L. Kergosien, and T. L. Kunii. Surface coding based on Morse theory.　IEEE Computer Graphics and Applications, 11（5）:66-78, September 1991.

〔4〕Y. Shinagawa and T. L. Kunii. Constructing a Reeb graph automatically from cross sections. IEEE Computer Graphics and Applications, 11（6）:44-51, November 1991.

〔5〕Y. Shinagawa and T.L. Kunii. The homotopy model: A generalized model for smooth surface generation from cross sectional data. The Visual Computer, 7（2-3）: 72-86, 1991.

〔6〕Y. Shinagawa and T. L. Kunii. Unconstrained automatic image matching using multiresolutional criticalpoint filters. IEEE Trans Pattern Analysis and Machine Intelligence, 20（9）: 994-1010, September 1998.

〔7〕Y. Shinagawa, T. L. Kunii, A. G. Belyaev, and T.Tsukioka. Shape modeling and shape analysis based on singularities. International Journal of Shape Modeling, 2（1）: 85-102, 1996.

〔8〕S. Takahashi, T. Ikeda, Y. Shinagawa, T. L. Kunii and M. Ueda. Extracting features from discrete geographical elevation data with topological integrity: Algorithms for extracting critical points and constructing topological graphs. Computer Graphics Forum （Proc. Eurographics ’95）,14（3）: 181-192, 1995.