Accumu Vol.6

不変埋蔵法とシステム同定

カリフォルニア州立大学フラトン校　ロックウェル国際教授

ハリエット・H・カギワダ Harriet H. Kagiwada

（翻訳　金沢工業大学情報科学研究所所長　川田 剛之）

Ambarzumianが1943年に大気散乱問題の研究への一つの新しい考え方[1]を提案したことが，Richard BellmanとRobert Kalabaによる可能性に富む”不変埋蔵原理と非一様媒質中の伝播”という論文[2]発表の契機となっている。著者達はその方法はいわゆるダイナミック・プログラミングの決定機構不要バージョンであると指摘している。

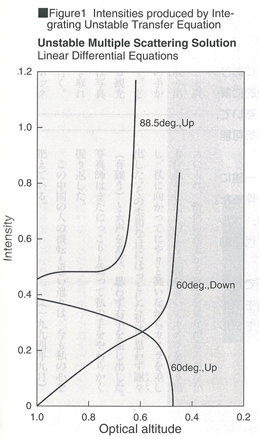
その基本的なアイディアは一つの新しい過程の集合の中に，ある与えられた物理過程を埋め込むことにあり，これにより埋め込を通して不変過程を得ることが可能となる。簡単のため，その両端をt＝0とt＝Xとする長さXの非一様な棒の中における粒子散乱という一次元の問題を考えてみる。棒端t＝Xに単位1の入力があるときの棒内の粒子の内部フラックスは伝統的な解として表現されてきた。しかし，その解は残念ながら不安定である（図1参照）。

不安定性は問題を最初から初期値問題として定式化することにより回避できる。不変埋蔵法は新しい解析的定式化を与えるのみならず，計算手法としても魅力的である。それは変分問題[5]だけでなく，線型，非線型の境界値問題[3]や積分方程式など[4]に適用可能である。不変埋蔵法は（2点境界値問題を）微分方程式に対する安定な初期値問題へと導く。その応用は中性子の輸送，幅射の多重散乱，温室効果温度，波の伝播，流体力学，その他数多くの物理過程や数学的解析などが含まれる。

直接問題に対する計算上のメリットに加えて，不変埋蔵方程式はシステム同定，或るいは逆転問題にも適している。ここで，逆転問題とは未知の物理パラメータを直接的な観測知識に基づいて最適に推定することをいう。

直接問題

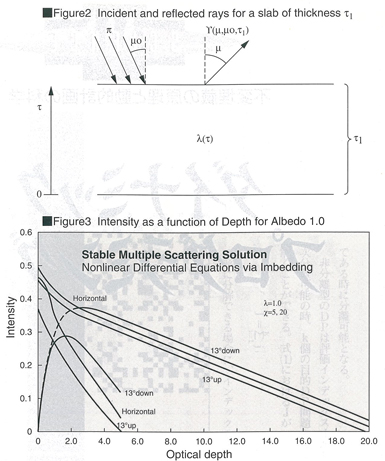
図2に示す様に，平行光線が上方から一様に平行平面な非一様媒質を照射するときの拡散反射について考える。反射関数は初期条件を持つ微積分連立方程式を満足する。その微積分方程式の系は例えば7点のガウス積分の様な高次の求積公式を用いて高精度に近似できる。即ち，7×8／2＝28個（本来7×7=49個であるがその対称性によりこの個数になる）のRiccati型の非線型微積分方程式から成る系はX＝0からX＝T（任意の最大厚さ）の範囲で積分される。その計算結果は表とグラフの形で図3に示されている[6]。これまで不安定な2点境界値問題の解として扱われてきた内部強度関数は，この様に不変埋蔵法により簡単に扱うことができる。同様に，源泉関数に関しても，不変埋蔵法はうまく解けない条件にある積分方程式を解く必要性を回避する。

系同定[7]

不変埋蔵法は逆転問題に適した定式化，即ち微分方程式系の初期値問題に福音を与える。物理過程の研究において基本的な問題は観測を最もよく説明する物理過程のパラメータを推定することである。前述の例では，その未知のパラメータは媒質内の光学的厚さや単散乱のアルベド（反射率）の変化である。これらのパラメータは微分方程式系を記述する部分に現れる。このタイプの逆転問題は系の同定問題と呼ばれる。そして系同定問題は普通は非線型である。系の記述自身が非線型であるかもしれないし，与えられた直接問題が，たとえ線型であったとしても系に未知パラメータを導入することにより問題は一般的に非線型になってしまう。

準線型化は非線型の多点境界値問題を解くために考案されたテクニックであり，逆転問題にも役に立つものである。このテクニックは非線型の微分方程式系に対するニュートン法の拡張といえる。準線型化はそれ自体，偏微分の評価と完全な初期パラメータ・セットの推定を必要とする。もし，初期推定が良ければ，推定は二次式で収束する。長い間，これら二つの要求は準線型化法を簡単に実現する場合の障害となってきた。しかし，現在では計算機による偏微分の評価については，Feed法[8]などが使用でき，パラメータの初期値推定は連想記憶を持つニューラル・ネットワーク手法[9]を通じて直接的に行える様になっている。

最後に，Bellman - Kagiwada - Kalaba - Sridhar等[10]の逐次推定に対する非線型フィルターは不変埋蔵法を用いることにより発展したことを特に挙げておきたい。

References

1. Ambarzumian, V.A.,“On the Scattering of Light by a Diffuse Medium,"Compt. rond, Doklady Acad, Sci URSS, 38, 257, 1943.

2. Bellman, R. and R. Kalaba, Proc, Nat, Acad. Sci. 42, (1956)629-632.

3. Kagiwada, H. and R. Kalaba,“Derivation and Validation of an Initial-Value Method for Certain Nonlinear Two-Point Boundary-Value Problems," J. Optimiz. Theory and Appl., 2,378-385, 1968.

4. Kagiwada, H. H. and R. E. Kalaba, Integral Equation via Imbedding Methods, Addison-Wesley, 1975.

5. Kalaba, R. and K. Spingarn, Control, Identification, and Input Optimization, Plenum Press,1982.

6. Kagiwada, H., R. Kalaba, and S. Ueno, Multiple Scattering Processes: Inverse and Direct, Addison-Wesley, 1975.

7. Kagiwada, H., System Identification : Methods and Applications, Addison-Wesley, Reading, 1974.

8. Kagiwada, H., R. Kalaba, N. Rasakhoo, and K. Spingarn, Numerical Derivatives and Nonlinear Analysis, Plenum Press, 1986.

9. Kagiwada, H., J. Kagiwada, and S. Ueno,"Kalaba's Associative Memories for System Identification," Applied Mathematics and Computation, 45, 135-142, 1991.

10. Bellman, R., H. Kagiwada, R.Kalaba, and R，Sridhar,"Invariant Imbedding and Nonlinear Filtering Theory," J. Astronaut, Sciences, 13, 110-115, 1966.