Accumu Vol.3

連想記憶モデルによる情報の最適識別

カリフォルニア州立大学フラトン校ロックウェル国際教授

H・H・カギワダ

京都大学名誉教授・金沢工業大学名誉教授

京都コンピュータ学院情報科学研究所所長

上野 季夫

はじめに

情報の観念から脳を研究するには，神経回路モデルを用いて，脳の機構を解明するのが適当である。ここでは生体の記憶機能に対象を限定してみよう。何故ならば，一般的観点からの解析には多大の紙面を要するからである。また医学的観点による脳のモデルについては，西丸博士による解説，及び神経回路モデルについては，杉坂博士の解説があるので極力説明の重複をさけることにする。

生体は非常に長い系統発生の中で形成されたので，進化の過程中に得られた適応は複雑な構造形態を生じた。換言すると，いろいろの感覚記号及び情報処理のために，その神経領域は特殊化されてきた。大脳研究には大別して2つある。その1つは記憶の化学理論に基づいて，記憶分子は神経細胞内の細胞質の内にあるという。他方の説によると，神経回路網は適応的フィルター（濾波器）として，且その集団的伝達特性は信号により変化するという。ここで考慮の適応的連想記憶の回路網はその一例と考えられる。

神経回路網は，生後の経験や学習により，自己の現在の環境に適応する様に，次第に生長してゆく。この際外部からの刺激の付加により，神経細胞間に新しい結合やその強度の変化がおこる。これは神経回路の自己組織化と考えられる。

連想記憶のシステム・モデル

連想記憶のモデルはいろいろな条件に対し，対応できるものでなければならない。例えば，（イ）最も単純な生体回路網，（ロ）発生した記号のみによる連想の形成，（ハ）記憶した事象の構造化した系列の表現法，（ニ）想起した情報に基づく検索過程，等がある。連想の概念を一般的な形式で定義すれば，抽象的構造全体を連想記憶と定義してよいであろう。

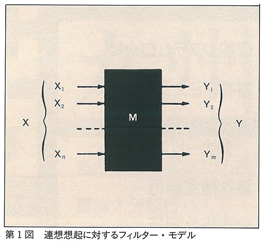
生物学的情報処理の演算は，（1）選択的蓄積と，（2）選択的想起によると考えられる。図1は記憶の最も簡単なシステム・モデルを示す。これは入力回路と出力回路を結合している記憶媒体からなるとする（第1図参照）。この種の記憶の特徴は，入力回路に生じた信号模様をその内部状態に保持する能力を持っていることである。

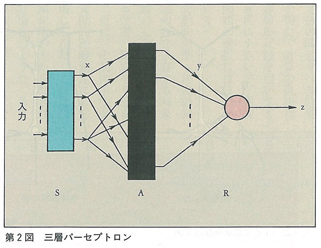
この学習過程には，教師ありと教師なしが考えられる。前者では，神経回路は，外部の教師から教えられる情報を利用して，自己組織化を進めてゆく。この教師あり学習モデルとして，ローゼンブラットの提唱による，三層構造を持つパーセプトロンが有名である。ここの第一層目は視細胞が並んだ入力層S，中間層はA細胞という細胞層，第3層はR細胞と呼ばれ，認識結果を出力する出力細胞である。学習時には外部の”教師”はパーセプトロンに学習模型を表示し，R細胞の出力を観測し，その表示を調節する機能を有する。

生物学的記憶に独特な検索の原理は，情報の連想性想起である。計算機の記憶では，その記憶を貯えた場所を指定することによって行われている。入力に対し型化された刺激（K）が与えられると，そのKと連想した特定の反応模様が出力Rとして得られる。その際刺激が生じたときの前後関係（又は分脈）（C）を表す付加的情報も与えられる。

いろいろな刺激による分脈（C）を用いることにより，想起する項目の指定を制限することが可能である。更に相関行列のような連想記憶モデルに対し，想起出力を再び入力側に正帰還するような経路を付加できる。これはコホーネンにより正帰還附相関行列型連想記憶と呼ばれる。

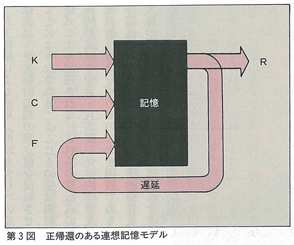
単純な連想記憶のシステム・モデルとして，4種の情報の路線が考えられる（第3図参照）。3個の入力路線から，同時に情報記号値が，記憶の内に転送され，1つの出力路線から想起模様が現れる。これは遅延帰還として第3の入力になる。総括すると，時間変数tを指数とする検索型入力K（t），同時発生型入力C（t），更に遅延帰還の経路を通じて，第3の入力F（t）がある。上記のモデルは，学習による識別決定の神経層状回路モデル・パーセプトロンに類似である。

連想写像と連想記憶

一般に連想性想起は有限個の入力ベクトルを一定の出力ベクトルに変換する写像であると定義できる。もしこの想起が誤差の少ないものであれば，入力ベクトルの近くにあるベクトルはその出力ベクトルの近くに写像される。ここに於いて線形連想写像によれば，参照ベクトルからの確率的偏差が，想起の演算で最適修正されることを示す。

最適線形連想写像によれば，有限個の分値を持つ矩形行列xとyとは行列演算子MによりMXはyと等値される。xとyを既知行列として，未知行列Mに対する形式解はモアー・ペンローズにより与えられ，それは誤差に対する最小自乗近似解に相当する。

非線形連想写像を用いれば，線形変換ではその線形従属のため識別できなかった模様も識別できる。しかしその解析はより複雑になる。

連想性想起の基本的なものとして，自己連想性と相互想起性が考えられる。前者は一連の入力信号の全体がパターンとして記憶中に記名されたならそれをその任意の部分により検索可能である。後者はこのモードの演算に対しては，指定したキイ・パターンに対する反応として得られる出力は，この目的のために予約した指定入力を用いてその記憶をつくることができる。

計算機工学では連想記憶なる名称のもとで，内容番地法，ハッシュコード法のような装置がある。また写真の様な絵画的情報の集積に対しては，ホログラフイ連想記憶，及び同上によらない分布連想記憶がある。例えば抵抗回路網による相似型連想記憶である。これに対しては，線形写像が有効である。

連想記憶は人工神経回路網の理論から，訓練対の概念に基づくものである。計算例として衛星による地球画像を考える。k番目の訓練対は，k番目の媒質の助変数を考え，且k＝1，2，・・・，kに対し，その媒質に対応して観測の組をつくることにより作製される。ここにk番目のパラメータ・ベクトルはa_kであり，その分値は地平面のアルベド（輻射反射率）及び他のシステム・パラメータである。観測値は反射強度S_ik(i＝1，2，・・・，7）。ただしiは反射方向を示す。そこで観測行列Sをつくる，パラメータ・ベクトルからパラメータ行列Aをつくる。そこで行列M中におけるこの情報を要約すると，行列MSはAを近似することである。これは記億行列Mを決定して，左辺における分値と右辺における分値の差の二乗の和が極小になるようになることを意味する。最小自乗論により。

M ＝ AS_＋　　　（1）

上式中，S_＋は刺激行列Sのモアー・ペンローズの一般化反転である。一度行列Mが決定されれば，観測ベクトルyが観測から得られるとき，次式をうる。

a ＝ My　　　（2）

ベクトルaの第一分値はこの観測に対するアルベドの推定である。

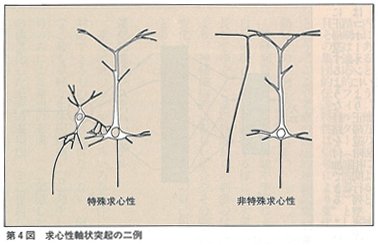
最適連想写像，パターン認識，生物学的連想記憶等多くの重要な機能はいかに共に作用するかは興味があり，且重要な研究の分野である。これらの統一的皮質記憶のモデルとして，層状神経回路が考えられる。それらは新皮質，外部皮質，小脳，神経節等にみられる。かかる層状組織は特別な求心軸索突起の周辺に形成される（第4図参照）。

連想記憶モデルによる情報の最適識別

衛星による遠隔探査とその大気補正

人工衛星による惑星（地球を含む）の遠隔探査は，分光輻射輪郭の測定値を反転させることによりなされる。ここにその値は輻射輸達式により記述される。これらの反転式の伝統的形式は不安定，且実際の光学的性質及び地表面反射率を求めるのに大変困難である。今迄直接問題は，惑星大気の光学的特性及び大地の反射特性を与えて，我々はこれを非線形微積分方程式の系に対する初期値問題として取り扱った。高次のガウスの積分式を用いて，この系は初期条件を有する常微分方程式の系に帰せられた。これによって，安定系として，任意の厚さの大気に対し数値結果を与えた。

遠隔探査の問題は，反転問題として，各点の輻射場の値を与えて，その光学的特性及び地表面反射特性を求めることである。この目的に対し，準線形化法により，最適値から2割又は5割も異なる推定値から始めて，そのパラメータの推定の改良が実施された。必要とされたものは，第一近似を得る体系的な方法である。

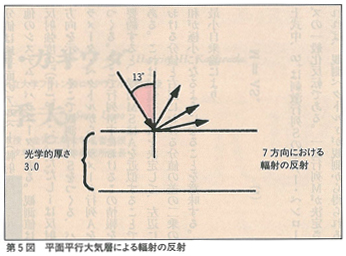
数値計算例：平面平行，均質大気が不完全吸収体の底面に接しているとする。今平行光線がその大気上面に入射する。その入射光線の角は13度とし，その大気の光学的厚さは3.0とする。大気上面における分光拡散反射光は7つの反射角で測定される。これらの測定は－1から＋1の間に均質に分布した確率雑音を含んでいる。我々の問題はこれら7個の雑音入りの観測からその反射アルベドを推定することである。

実際にはアルベド0.1，0.2，・・・，1.0をもつ10個の場合に対する連想記憶を取り扱う。これらの場合，n＝0.05をもつ7個の雑音の入った反射強度が含まれている。これらの実験の場合から，行列Mが実験の知識を総括するように決定される。我々の得た行列はM＝(7.5，－3.8，－0.9，2.6，2.1，3.5，－9.3)そこで50回のモンテ・カルロ実験を行って，真のアルベドが0.1，0.2，・・・，1.0である時の7個の雑音入りの実験をシミュレートした。これらの測定における雑音はn=0.01であった。そのアルベドの平均推定値は各々次の如くであった。

0.09，0.18，0.27，0.37，0.47，0.58，0.70，0.82，0.94，及び1.03

これらは真の値に近い。他の実験ではn＝0.10になる迄観測値に雑音を入れたが，その訂正したパラメータは不正確になった。その時点でポギオによる非線形連想記憶を用いて，推定値の満足すべき結果を得た。計算の負担は非線形記憶を用いても，非常に小さいが，訓練問題の選択には技巧がいる。

受動的照準：角度の測定のみに依存する対象面の二次元空間における位置の測定を考える。

更に，上記の手法を受動的距離測定にも応用してみた。これは観測が塔の上からなされた場合のように，角度のみに依存する，二次元空間における対象物の位置測量の古い問題である。上記の連想記憶の手法を用いて，満足する結果を得た。

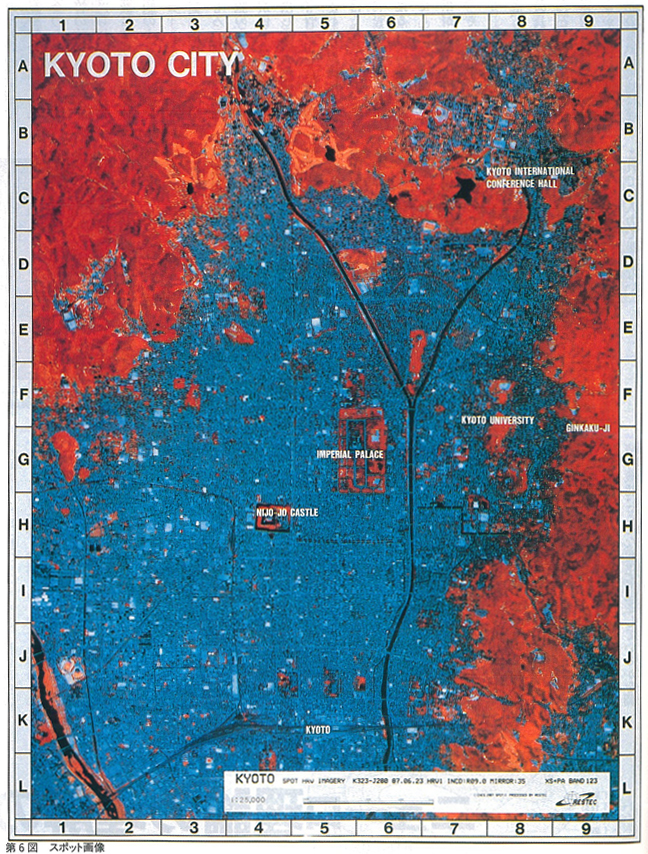
リモート・センシング画像の例として，1987年6月23日に取得された京都市付近のスポット画像を示す。

おわりに

神経回路網モデルを用いて，情報工学の諸問題を取り扱うようになったのは，近年のことである。医学的観点からは，まだ多くの未解決の問題を含み，その取り扱いは容易ではないようである。他方情報工学の観点からは，たとえ簡単なモデルを用いても，従来の解法に比して，有力な手段を提示し始めている。将来の数学的及び工学的発展の期待できる分野と思われる。

尚本稿はK.Kagiwada（カリフォルニア大学サンジエゴ校研究員）及びR.Kalada（南カリフォルニア大学教授）の二氏との共同研究によるものである。