Accumu Vol.2

世のなか，非線形

東保 光彦

パリで開かれた数学の国際会議で，ソ連数学界の大御所ポントリャーギン（1）がおこなった最適制御理論の講演に対し，反戦運動家としても知られる，フランスの数学者グロタンディーク（2）が

「あなたの理論は，戦争に利用されるのではないか」

となじった。これに答えて，ポントリャーギンいわく，

「戦争は非線形なので，わたしの線形理論は役にたたない」

立命館大学の学生のころ，京都大学から来ておられた森毅先生にうかがった話である。20年ほど前のことで，このとおりの内容であったかどうか自信がない。そのときには，まだ，非線形なるものが何か，よく知らなかった。

素粒子論にも，非線形スピノル方程式というのがある。ハイゼンベルグ（3）が統一場理論の出発点にしたのがそれである。しかし，私どもを指導しておられた江夏弘先生は，「ハイゼンベルクは間違っている。基本方程式が非線形であるはずがない」と，この理論をきっぱり否定しておられたし，おそろしく難しそうでもあったので，あえて勉強する気も起こらなかった。ただ，当時の風潮であったのかも知れないが，なんとなく，「非」とか「反」とかのついた言葉に，漠然とした魅力を感じていたように思う。

▼線形と非線形

線形と非線形とは，どこが違うか。まっすぐなものが線形で，曲がったものが非線形である。数学で言うと，直線や平面は一次方程式で表すことができることから，一次方程式で表すことができるものは，すべて，線形であるという。線形代数の美しさは，単純さにある。それはまた，すっきりとして明快である。

ところが，この世の中は，曲がりくねったもの，ねじくれたもの，歪んだもの，不透明でややこしく，わかりにくいもので満ちみちている。これらを，ひとことで表す数学の言葉が，非線形である。われわれが日常生活している世界は，したがって，非線形であることがほとんどである。

▼非線形システム

世のなかで非線形なのは「もの」だけでない。「こと」も非線形であるほうが多い。「こと」のなりゆきが予想外に展開して，なかなかつかめないのは，そのためであろう。ポントリャーギンは，戦争という「こと」が非線形であると言ったのだ。「もの」と「こと」をいっしよにして，システムという。たとえば，振り子という「もの」と，それがゆれる「こと」をいっしよに考えると，振り子のシステムができる。「こと」が非線形であると，システムも非線形であるという。

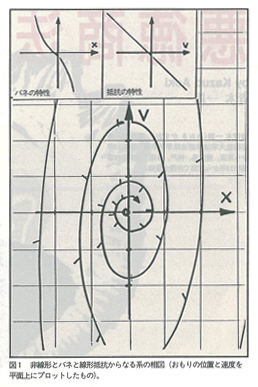
「こと」のなりゆきが，たまたま微分方程式で書き表せたとしよう。すなわち，考えている対象の状態を表す関数と，その状態の変化率（時間で微分したときの導関数）との関係を方程式で表せるということである。この方程式が，関数とその導関数について一次式であれば，これは線形システムで，解法もよく研究されている。線形システムの例として，バネの端につけたおもりの振動が，よくひきあいに出される。しかし，現実には，これも線形になることはめったにない（図1）。「微小振動は線形で近似できる」といえるぐらいなものである。世の中の現象を表す微分方程式は，残念ながら，ほとんどが非線形であるといってよい。しかも，非線形の微分方程式が厳密に解けるのは，ごく限られた場合だけで，たいていは，コンピュータにより，数値的に近似解を求めるほかないのが現状である。

▼混沌の死

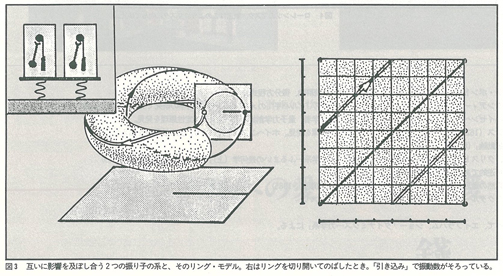
とはいえ，非線形システムの研究は古く，これまでにも，システムの興味深いふるまいがいろいろ見つかっている。たとえば，「引き込み」現象もそのひとつである。クォーツの時計があたりまえになった今では，あまり見られなくなったが，時計屋さんの壁にかかったゼンマイ式の柱時計が，一斉に時を打っている光景を思い出す（図2）。別々にしておくと，異なった進み方をする時計を，同じ壁にかけると，互いに影響を及ぼし合って，振り子の運動がそろってくる。ホイヘンス（4）が見つけたという，この現象を「引き込み」とか「同調現象」という。「引き込み」現象がおきるメカニズムは，計算でも示されるが（5）R・エイブラハムの「ダイナミクスーふるまいの幾何学」（6）に，巧妙に図解されている（図3）。

混沌とした状態（カオス）から，「引き込み」によって秩序（コスモス）が生まれる，という図式は，なかなか魅力的である。原子の雲から分子が生まれ，分子から生命体が生まれ，それが進化して，複雑きわまりない人間が出現したように，無秩序から秩序へ向かう道は，世の中が発展して行く方向を示しているように思えるではないか。ところが，この方向は，熱力学の基本法則に反している。コップの中の水に，インクを一滴落とせば，インクは水と混じりながら徐々に広がって行く。これは，熱力学の第二法則（7）によれば，インクと水からなる系のエントロピーが増大した，ということになる。エントロピーは，乱雑さのことであると思えばよい。つまり，秩序あるものも，時がたつと，だんだん無秩序になってゆく，というのが第二法則である。

熱力学の第二法則に反して，無秩序から秩序が生まれる現象が，世の中にはいっぱいある。結晶の成長，砂丘の風紋，生物の発生や形態形成，国家の形成などは，その例である。H・ハーケンは，このように協調によって秩序が生まれ，組織化される現象の研究をシナジェティクスと呼んでいる（8）。シナジェティクスは，したがって，非線形システム研究の一分野だといえる。

▼コスモスからカオスヘ

非線形システムのふるまいで，最近注目を集めているのがカオスである。カオスは通常，混沌，混乱状態，無秩序などと和訳されるが，数学では特別な意味を持っている。厳密に定義された微分方程式や差分方程式の系から，まったく予想もっかない事態が生まれてくることがある。これを力オスと呼んでいる。微分（または差分）方程式と初期条件が決まっていると，未来の状態も完全に決まってしまう，というのが常識である。初期条件を少しくらい変えても，ものごとはほぼ同じように進展するであろう。線形システムの世界では，確かにそうである。しかし，非線形システムでは。一般にそうでない。僅かな初期条件の違いから，まったく異なった状況がうまれる。とはいえ，まったくデタラメになるのではない。数学でいうカオスには，規則正しいふるまいとランダムとの中間といったイメージがあてはまる（9）。

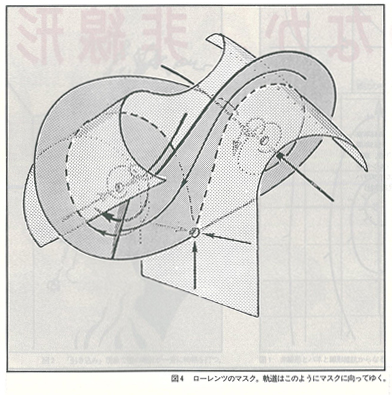
カオスの例では，「ローレンツのマスク」が有名である（図4）。これは，地球物理学者のエドワード・N・ローレンツが，大気の乱流モデルをコンピュータでシミュレートしていて発見した。全体のマスクの形は保たれるのに，それぞれの軌道がどのように進むかは，予想できない。

▼神経の鈍さ

ニューロ・コンピュータの研究が盛んになって，コンピュータ技術者のあいだにも，神経細胞の性質がとり沙汰されているが，神経の応答が非線形であることも，古くから知られている。神経の応答が，もし，線形であれば，どんなにわずかな刺激にも反応する（刺激を伝達する）はずである。しかし，神経は，わずかな刺激には反応しない。刺激が，ある程度強くなってはじめて，反応するのである。つまり，神経には，ある種の「しきい」があって，刺激の強さがその「しきい」を越えないと，刺激を伝達しない。「しきい」を高くすると，神経は鈍くなる。ニューロ・コンピュータでは，「しきい関数」なるものを定義して，このしくみを取り入れている。それゆえ，ニューロ・コンピュータは，非線形システムのカオス的な複雑さを，そっくり抱え込んでしまう結果になった。ニユーロ・チップのような「もの」はできても，理論はさっぱり，という状況は，とうぶん続くであろう。

（1990・3・15）

註

（1）レフ・セミョーノヴィチ・ポントリャーギン（1908-）位相幾何学，連続群論，微分方程式論などで多くの先駆的業績がある。

（2）アレクサンドル・グロタンディーク（1928-）フランスの数学者グループ”ブルバキ″のメンバー。代数幾何学の研究でフィールズ賞受賞。

（3）ウェルナー・カール・ハイゼンベルク（1901-1976）ドイツの理論物理学者。量子力学創始者の一人。不確定性原理を発見。

（4）クリスチャン・ホイヘンス（1629-1695）オランダの物理学者。土星の環を発見。ホイヘンスの原理により，光の波動説を唱えた。

（5）たとえば，戸田盛和『振動論』（培風館　1968）

（6）ラルフ・エイブラハム，クリストファー・ショー共著「ダイナミクス－カ学系－ふるまいの幾何学（上）」（東保訳，現代数学社　1989）

（7）巨視的な動的現象は不可逆的である，とも表現される。

（8）ヘルマン・ハーケン「自然の造形と社会の秩序」（高木隆司訳，東海大学出版会　1985）

（9）山口昌哉「カオスとフラククル－非線形の不思議」（講談社　1986）に詳しい。

＊ここに掲げた図は，すべて，エイブラハム，ショー「ダイナミクス－力学系」による。