Accumu Vol.3

ファジィ理論と応用

大阪府立大学名誉教授

大阪工業大学教授

日本ファジィ学会長

浅居 喜代治

最近，ファジィ理論が大へん有名になり，いろいろの分野で応用され，それぞれかなりの成果をあげている。ファジィ理論は，まず集合についての新しい考え方が，1965年にカリフォルニア大学のザデー教授によって提案され，これを受けて，論理や推論，あるいは測度へと発展してきたものである。現在，家電製品，カメラ，自動車などに実用化されているものは，推論を用いた自動制御である。

ここでは，初めに，ファジィ理論の考え方を述べ，次に応用について概説しよう。

ファジィ理論の考え方

ファジィ理論は，ヒトのあいまいな思考・判断のプロセスの模擬という目的を持っており，その実現には電子計算機が用いられる。この目的では，従来のディジタル計算機を用いることもできるが，高速化のために，ファジィ推論やファジィ演算を行うための専用の素子もいくつか作られている。

ファジィ理論は，ヒトのあいまいさの取扱いに重点を置き，経営者，管理者，ビジネスマン，技能者，専門家の主観的判断を活用しようとしている。ここでは，この意味で，ヒトのあいまいさについて考えてみよう。

ヒトの思考・判断について考えてみると，種々の状況や情報を，必要な程度に検知して，あらかじめ蓄えられている知識・経験と組み合わされて，ある結論を出していることが分かる。必要な程度に検知するとは，ヒトが知覚・判断するのに適当な程度ということで，これはかなり「あいまい」なものである。例えば，道路上を自動車－Aに続いて自動車－Bが走行しているものとする。Bのドライバーは，Aとの車間距離を安全の立場から適当に保っている。自分の基準よりも「少し長くなる」ことを視覚によって知ると，今までよりもアクセルを「少し踏み込む」し，逆に，「少し短くなる」ことを視覚によって知ると，今までよりもアクセルを「少しゆるめる」ようにして，車間距離を保つ。車間距離が「かなり開く」と，制限速度内でアクセルを「かなり踏み」，前の車に近づくし，また車間距離が「かなり接近する」と，ブレーキを「やや強く踏む」。このように，車間距離についての状況を，「少し」や「かなり」という言葉で示されているように，あいまいに検知して，自動車を同様にあいまいに制御している。ここで，「あいまい」という言葉を使っているが，日本では古くから，「あやふや」とか「でたらめな」などの良くないイメージで用いられてきたが，ここでは，そのような意味ではなく，必要な程度の正確さということである。ヒトは，きわめて多くの現象や問題の認識・判断を次々と行うために，柔軟に対応し，限られた感覚能力や知能を用いて，限られた時間内に思考・判断し，限られた言語によってその結果を表現しなければならない。このために，現象や問題をあいまいな形で把握し，かつあいまいな形で表現せざるを得ないと考えられる。この場合，ヒトはすぐれた感覚器官を備えていて，正確ではない動作をしても，その良否を検知してフィードバックを行い，動作の修正ができるから最終的には所期の目的を達成することができ，問題になることは少ない。別の例として，ヒトとヒトとの対話がある。ヒトの言葉にはあいまいさがあり，不明確という欠点はあるが，反面この言葉を受け取る側の自由度が尊重され，自主性を伸ばしたり，対人関係を好ましい状態にするなどの利点も多い。私どもが，かなり正確に把握できる現象や問題は，簡単・小規模なものだけであって，この場合，一般には限られた知識・経験や情報・データを用いて現象や問題を表現できるが，これが複雑・大規模になると，情報などが不十分であいまいさを伴うようになる。このとき，無理に正確に表現しようとすることは，かえって不正確になり，むしろヒトのように，あいまいに捉え，あいまいに表現することがかえって正しいといえる。

以上のヒトのあいまいさの数量化にファジィ集合論が用いられる。あいまいさの数量化と，その演算について次に述べる。

あいまいさの数量化と演算

ヒトの自然言語として用いられる「大変美しい」，「やや大きい」，「よい商品」などや，「美人」，「老人」，「優等生」などの概念は，明確に規定できず，個人的な主観でその認識に若干の差があり，あいまいである。このような表現を数学的に表わし，演算するためにファジィ集合論が体系化された。この集合論は，従来の集合論の拡張と考えられるもので，メンバシップ関数（Membership Function　略称－MF）を用いて，集合への要素の含まれる程度を表わす。

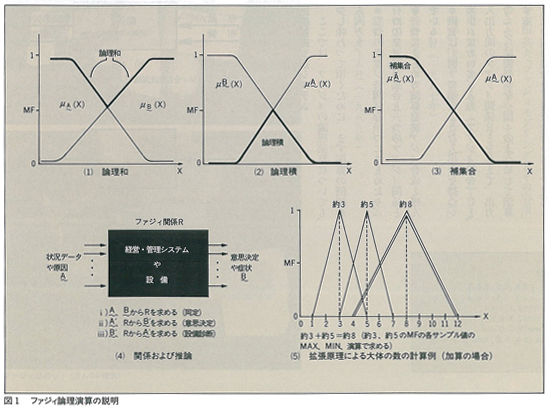
このように，私どもが日常用いている言葉が数量化されてコンピュータに入力されると，これについてファジィの論理演算が行われる。この場合，従来のディジタル型コンピュータのように正確な演算を行うのではなく，人間の言葉のもつ正確さに見合う程度のおおまかさで，ファジィ独得の論理演算を行わせる。ここでは，おおまかに演算するために，ソフトウェアの量が節約でき，また演算時間も短縮できる。この論理演算には，MFについての論理和・論理積・補集合や，関係・推論・拡張原理などの方法が用いられる。ファジィのソフトウェアを作るときには，具体的に演算法を理解する必要があるが，ここでは省略して，その概要を図1に示しておこう。

これらの演算をいくらかでも理解して頂くために，後で応用例を挙げて，そこで触れることにする。

ファジィ理論の応用と概況

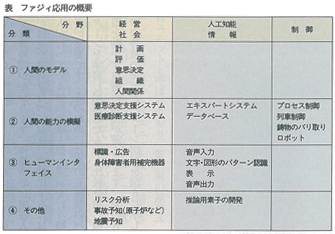
ファジィ理論は，ヒトのあいまいな知的情報活動の過程をモデル化することを出発点としているので，この立場から応用分野を分類すると次のようになる。

1，ヒトの知的情報活動のモデルを作って，ヒト個人や社会，組織の特性を調べたり，社会・組織・機器などの最適設計を行う。

2，ヒトのすぐれた能力（情報検索・処理）の模擬，専門家達の豊富な知識・経験（計画・評価・判断・決定・制御など）を活用する。

表は，この立場から分類して，応用の現状を示したものである。

応用のうち，制御は早くから実用化され，コントローラの製品も発売されている。これは，制御対象が複雑で，その数学モデルが作りにくいとか，非線形になるような場合に，従来は熟練作業者に依存していた分野に応用が進められている。簡単なコントローラを用いて，対象の特性の変化にも順応して人間らしい柔軟な制御を実現している。産業・社会・交通などの分野に広がりつつある。

次に，応用の盛んなのはエキスパートシステムである。この場合も，あいまいさに対してプログラムを複雑にせず，即座に，与えられた情報のあいまいさに見合う程度の正確さの答えを出すことができ，信頼できる点が好評である。産業・社会・医療・教育などの分野に広がりつつある。

以上の応用のうちから，制御分野については，洗濯機，医学分野については，医療診断支援システムの例をとりあげて簡単に説明しよう。

洗濯機への応用

現在，多くの家電製品にファジィ理論が応用されているが，そのほとんどが，ファジィ推論を用いる制御の応用である。現在のところ，ファジィ推論のプログラムを，既設のマイクロプロセッサに入れ，それぞれ適当なセンサーが用いられている。いずれ，高速を要する応用には，専用のファジィ推論素子が用いられるようになるだろう。以上の家電製品のうちで，洗濯機は，早く実用化が図られたもので，M社と，H社などから昨年発売され，好評を得ている。

ここでは，これらの製品について，概説をしよう。

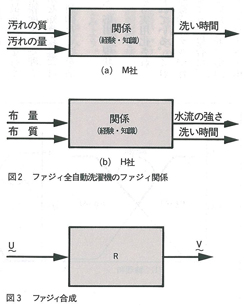
いずれも，全自動洗濯機であって，それぞれのセンシング情報（センサーで計測する量や質）と，制御量（制御される量）とを図示すると図2のようになる。

すなわち，M社の場合は，洗濯機の汚れの質（脂汚れ，泥汚れの程度）や汚れの量（軽い汚れ，ひどい汚れなど）をセンサーで検知し，これらの概括的なデータから洗い時間をファジィ推論で推定して，時間の無駄を省くと共に，洗濯物のいたみを防いでいる。また，H社の場合は，布量（多い，普通，少ないなど），布質（ゴワゴワ，普通，しなやかなど）をセンサーで検知して，水流の強さや洗い時間をファジィ推論で推定して，時間の無駄を省くと共に，洗濯物をいためず，きれいに洗うことを目指している。

両社共，効率化・経済性・ヒューマンファクタの3目標の実現にファジィ理論が活かされている。

医療診断支援システム

ここでは，ファジィの論理演算についても，少し味わって頂くために，まず演算の例題から入ろう。

2つのファジィ関係を1つにまとめたり，1つのファジィ集合と1つのファジィ関係とを1つにまとめる演算をファジィ合成と呼んでいる。

例えば，図3に示すような入出力を持つシステムにおいて，入力（ファジィ集合）Uと，入出力間のファジィ関係Rとを与えて，出力（ファジィ集合）Vを，図4のようにして演算する。

この例の意味を，医療診断の場合で説明しよう。図3において，Uは病因または病名，V_～は病状であり，これら両者の関係Rは医師の知識・経験によってあらかじめ与えられる。上例は，V_～が，患者の訴えとして，「少し熱があり（MF0.6），頭の後頭部がやや痛み（MF0.6），肩がかなり凝る（MF0.8）」となり，これに対して，医師が，「あなたは普通の風邪と思われる（MF0.8）が，いま流行の流感の疑い（MF0.3）もある」と答える場合に相当する。この場合は，関係Rと，Vとを与えて，病因か病名を探すことを目的としており，これはファジィ合成の逆演算の方法によって行われるが，ここでは，省略する。また，多くの病例についての，入出力U_～，V_～から関係Rを，あらかじめ求めておくことを同定（Identification）といい，医学に限らず，多くの分野での知識・経験の整理・保存として大切であり，このようなデータベースを持つエキスパートシステム（Expert System）は，機器や設備の故障診断や，経営における意思決定，制御などに用いられている。

以上においては，ファジィ推論を用いることにより，入出力の少しのずれに対応できるようにしている。

以上のようにして与えられた病因や病名は，複数個あり，それぞれに確信の度合いがMFで付けられている。このデータを参考にして，最終的には，人間である医師が診断を下すこととなる。この意味から，「支援」という言葉が付けられている。

おわりに

以上，ファジィの考え方と応用について概説し，特に応用例も挙げて，具体的な説明も行った。

ファジィ理論は，以上で分かるように，人間の概括的な知的思考活動のモデルを作ろうとするもので，これによって，専門家や熟練技能者の経験，知識をコンピュータにとり入れ，AI化を図る。ここで，人間の知的情報活動が概括的となるのは，与えられている知能容量や，時間の制限によるもので，ミクロ（木の小枝）を切り捨て，マクロ（木の大技，幹）に注目することによって，方向性を見失わないようにしている。

一方，このファジィのモデルを用いて，逆に，人間の知的行動や，人間の集まりである社会の状況，あるいは自然や植物の特性などを調べようとする研究も，科学技術庁を中心として進められている。

ファジィの研究が，制御やエキスパートシステムのみならず，人文，社会，自然科学の広い分野で活用されることを期待してやまない。

参考書の紹介

これからファジィの勉強をされる方のためにファジィ関係の参考書として，邦書の一部を紹介しよう。

理論的・基礎的なもの

●浅居，ネゴイタ（編著）『ファジィシステム理論入門』オーム社（1978年）

●西田，竹田『ファジィ集合とその応用』森北出版（1978年）

●水本雅晴『ファジィ理論とその応用』サイエンス社（1988年）

●本田，大里『ファジィ工学入門』海文堂（1989年）

●坂和正敏『ファジィ理論の基礎と応用』森北出版（1988年）

●西田俊夫『おはなしファジィ』日本規格協会（1990年）

●廣田薫（編著）『ファジィシステム』計測自動制御学会（1990年）

●田中英夫『ファジィモデリングとその応用』システム制御情報学会（1990年）

応用に重点のあるもの

●寺野，浅居，菅野『ファジィシステム入門』オーム社（1987年）

●菅野道夫『ファジィ制御』日刊工業新聞社（1988年）

●寺野，浅居，菅野『応用ファジィシステム入門』オーム社（1989年）