Accumu Vol.6

ダイナミック・プログラミング

台湾ユーアンジィー工科大学　米国カンザス州立大学

E・スタンレイ・リー E. Stanley Lee

（翻訳　金沢工業大学情報科学研究所所長　川田剛之）

ダイナミック・プログラミング（Dynamic Programing:DP）の基本的アプローチは他の殆どの最適化手法とは異なっている。DPの創始者であるR. Bellman博士はDPは埋蔵と反復計算の両方に深い係りをもっていると指摘している。埋蔵の概念の故に，DPの計算上の方向性は本質的に逆向きである。実際，DPは全体の過程を最初はひとつの一段階問題として取り扱うが，計算が進んでいくにつれて少しずつ段階を加えていく。

ダイナミック・プログラミングはよく知られた，強力な最適化の手法であるが，それはまた，既存の問題を再定式したり，また同じ問題を異なる観点から見るのに役立つ概念でもある。それ故に，ダイナミック・プログラミングの最近の発展についての議論では，最適化手法の観点と方法概念の両方について考える必要があると思われる。前者に関する最も重要な発展は多数の並列計算機の使用やファジイDP，そして非分離の多目的DPにおいて起きている。DPの概念は色々な場所に応用されているが，最も顕著な例は，人工知能における直感的な探索や悪条件で不安定な境界値問題の数値解においてのDPの使用である。

多目的DP

多くの研究者達は多目的DPについて研究してきている。多目的DPは決定を下す者にとって非常に役に立つだけでなく，それは近代制御理論の基本的な主題にもなっている。スペースの関係で，これについての詳しい解説をしないが，興味のある読者はLi and Haimesによる解説論文を参照するとよい。そこではかなり詳細な概説が述べられている。

別の現在行われている研究テーマは多目的再プログラミング（Multiple Objective de novo Programing）に関連したものである。そこでは与えられたサブ・システムを最適化する代わりに，オリジナル・システムを最適設計することが重点的になされている。DPとファジイ概念の結合により実りある方法を得ることができるのである。

非分離型のDP

DPは色々な問題の最適値を見つけるために使われるが，本来のDPは分離可能性と単調性に関する条件を満足する問題にその応用が限定されている。最近，非分離の多段階問題に対する応用DPの手法が開発されている。その方法はk次の分離可能性概念と多段階DPを使用することに基礎を置いている。

典型的な多段階の最適化問題は次の様に表すことができる。即ち，

評価インデックス

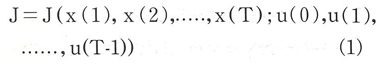
を次の条件

で，最大化または最小化する問題となる。

ここでx(0)は既知または与えられる値であり，Tは有限時間または最終段階を表し，x(t)∈Rⁿはシステムの状態，u(t)∈R^pは制御を表しており，また関数

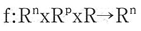
はn次元のベクトル関数である。

マルコフ過程の問題に対して，評価インデックスJは分離できなければならない。インデックスJは関数h_t, t=0,1,2,…が存在し，

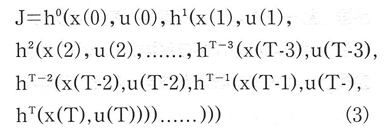
である時に分離可能となる。

非分離型のDPは評価インデックスJがk次分離可能の時，k個の目的DP問題として解くことができる。式(1)におけるJが

の形に分解できる場合に，インデックスJがk次分離可能という。ここで，j_i, i=1,2,…,kは式(3)の意味において分離可能である。

ファジイ・ダイナミックプログラミング

DPの方法は確率システムやファジイシステムに最適である。実際，DPは確率システムのために元来開発されたものである。こうして，最初のファジイ最適化方法はDPを使用して行われたということは驚くに値しない。別のかなり広範囲のファジイDPに関する研究はKacpzykによって行われている。そこでは多段階のファジイ・システムがDPの概念を使用して最適化されている。

大規模並列計算

記憶場所と計算時間の両面から多大な計算要求のために，大規模な並列計算機はDP最適化問題を解くのに最適である。最近，AngelとLeongは並列計算機上でDPを使用して楕円偏微分方程式を解いている。DPを用いると，うまく解けない微分方程式や不安定な境界値問題が解けるという利点はよく知られている。然しながら，計算時間が非常に長くなるのでDPは偏微分を解くには効率的ではない。大規模並列計算機を使用することにより，これらの問題のいくつかは解決できる。

人工知能における探索

直感的探索問題は人工知能の問題を解く場合に大変重要な役割を果たしている。Zの最良かつ最初のアルゴリズムとして知られている最適探索問題はDPの概念に基づいて形づけされている。うまく解けない，及び不安定な微分方程式や偏微分方程式の解はDPの概念を用いた別の例としてあげられる。