Accumu Vol.3
放射線医用画像の解析
東京大学工学部教授 藤村 貞夫
はじめに
物体が3次元に分布しているとき,その分布の非接触・非破壊測定には通常間接測定が用いられる。固体中の3次元分布では元々直接測定を非破壊で行うことが不可能であるし,固体中でなくても直接測定は対象とする分布に影響を与えずに実行することは極めて困難だからである。
固体中の3次元分布測定の内,最もポピュラーなものがX線CT(Computed Tomography)である。これはX線の透過を利用して吸収物体の2次元(面)分布を逆問題を解いて求めながら,順次面に垂直方向に走査して3次元分布を得るもので,X線の透過を利用することから透過形CTと呼ばれる。X線CTは医療の分野で極めて広く用いられ,臓器や組織の形態に関する情報が詳細に得られるため,診断のための有力な手段として活用されている。測定原理等の詳細は,既に多くの場所で解説もされているのでここでは触れない。
このX線CTに対して,それ自身が放射を射出する放射源の3次元分布を測定対象としてCT技術を用いる測定法は放射形CT(Emission CT略してECT)と呼ばれる。
X線CTを観測系にX線源をもつという意味で能動形CTと呼べば,放射形CTは対象からの放射を利用する受動形CTと呼ぶことができる。
放射源
それ自身が放射を出す放射源の主なものには,陽子を放出する放射性同位元素と,γ線を放出する放射性同位元素がある。前者はサイクロトロンを用いて作られる,人体構成元素の放射性同位元素,すなわち,炭素(11C)や酸素(15O),窒素(13N)等を人体に吸収させたとき,β崩壊で放出される陽電子(positron)が電子と衝突して消滅する際に放出する光子(γ線)を利用するものであり,一方,放射性同位元素(RI)からのγ線を利用するのが後者である。これらの他,もっと一般には,赤外線,マイクロ波吸収物体からの赤外線,マイクロ波などが考えられ,さらには,それ自身がエネルギーを放出する放射源ではなく他からの放射を反射・散乱する物体(2次放射源)であってもよい。
上記放射性同位元素を放射源として利用する放射形CTは,医学や生理学の分野で用いられるが,位置や形態に関する情報を得る透過形CTに対して,人体内に注入されたRIの分布を測定することにより,組織の生理学的な機能の情報を得ることができるという特徴がある。RIが特定の部位に集まるのは,体内でRIが移動することによっているが,RIの体内移動は循環,拡散による物理的移動と,摂取,排泄による代謝性移動がある。RIの静的な分布を測定することによって位置や形状に関する情報が得られるばかりでなく,RI分布の時間変化から体内移動を測定することにより,各種臓器の代謝などの生理的機能に関する情報を得ることもできる。
RIを種々の物質と化合させることにより,所望部位のみ選択的にRI濃度を高めることや,特定の物質の代謝のみを選択的に特定すること,特定の臓器に対する物質の集積・排出を時間的に追うこと等ができ,これによって,病巣の存在,位置,大きさ,形などを確認でき,また,臓器の機能の異常を調べることができる。たとえば,RIとして広く用いられるテクネチウム(99mTc)は半減期が約6時間で,これを無機化合物,無機錯体などとした薬剤として用いることにより,薬剤毎にそれぞれ,甲状腺や肝-胆系,あるいは,脳-血液関門,肝・脾臓・骨髄・リンパなどでの機能の異常診断のためのRI静的分布像,あるいは,その時間的変化を得ることができる。
このような目的に用いられるRI分布の測定・イメージングシステムとしては,目的に応じて種々の要求がある。病巣の位置,数の確認,背景の分離などに対しては,高い空間的分解能(深さ方向を含む)が,また,動態機能の測定に対しては高い時間分解能が,さらに,放射の統計的変動,放射線の人体への影響を少なくするためには放射線の高い利用効率が要求される。
放射形CTにおける投影
放射形CTは,その動作に基づいて,ポジトロンECT(PET Positron ECT)と単光子ECT(SPECT Single Photon ECT)に分類される。前者では,陽電子の放出に伴い,陽電子の電子との結合による消滅で,その近傍から光子[消滅γ線]が2個互いに正反対の方向に(ほぼ一直線上に)放出されることを利用して一直線上にある1対の検出器を用いる検出・測定系が使用される。単光子ECTにおいても,コリメータを用い,極く細い筒状の領域からのγ線を集める測定系が用いられることも多い。これらはいずれも線積分で表わされる投影を求めるもので,原理的には透過形CTと同じであるため,多くの方向からの観測を必要とし,しかも,一度にはある断面についての情報しか得られないという問題がある。なお,2次元分布を求めるために解くべき(逆)問題は透過形CTと同様である。
これらに対して,単光子ECTでは,放射形であることを利用してより簡便な測定系が利用できる。ここで述べる符号化開口ECTがそれである。符号化開口ECTでは,投影が,後で述べるように,線積分形ではなく,放射源による開口の陰を積分した形の投影であるため,観測が一方向で済み,しかも面を逐次走査することなく,3次元の分布が得られるという特徴がある。
符号化開口ECT
筆者らはこれまで,符号化開口ECTにおいて,性質のよい疑似乱数配列・M配列を符号化開口に適用したECTの性能評価やそれに基づく改良について検討を行ってきた。この形のCTは,観測系が簡単で,一方向から一度の短時間の観測のみで3次元分布に関する情報が得られるという極めて大きな利点がある反面,深さ方向の分解能が低いという点で問題が残されている。この問題を従来の利点を余り大幅に損なうことなく解決することが現在の目標である。ここでは,符号化開口ECTの原理を述べ,それによる測定結果とその問題点を示した後,この問題を解決する方法の概略を述べる。その方法として,観測に極く少数の複数投影を利用し,像の再構成に反復法を用いる方法を現在開発中であるが,その詳細は割愛する。
以下では光路中での放射の吸収・散乱は無視できるものとし,また,放射の持つ波長が短くて開口による回折が無視できるものとして議論する。このような条件を近似的に満たす放射としてここでは放射性同位元素RIから放出されるγ線を用いる。実際には,吸収・散乱による減衰が存在するがこれを無視している。
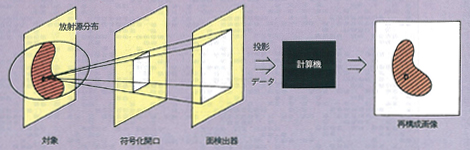
図1 符号化開口ECTシステム
符号化開口形のECTシステムのブロック図を図1に示す。このシステムは測定系と観測データに基づく像再構成系(計算機)からなる。測定系は,ある規則に従って開口が形成された符号化開口とシンチレーションカメラなどの面検出器からなる。測定においては,放射源からの放射により,開口の影が面検出器上に形成され,これを面検出器で2次元投影データとして得る。像再構成系では,この投影データから,深さ方向にある面を仮定しながら,計算機による演算で断層像を得ていく。投影データの性質を明らかにするため,深さ方向に開口面と平行な面を考え,その上にある放射源による投影信号を考える。面上に2つの放射源があれば,それらによって作られる影は平行移動した開口の形を重ね合わせたものとなる。一方,深さの異なる2つの放射源による影は,倍率の異なる開口の形を重ね合わせたものとなる。このように,投影信号には,深さの情報が影の倍率として,横方向の位置の情報が平行移動量として含まれている訳である。こうして得られる投影信号から,深さと位置を求めることが再構成の問題である。
ここでは,マッチトフイルタの方法を用いて再構成する方法を示す。これは,符号化開口に特殊なパターンを用いることにより,再構成のための演算を簡単化するもので,そのためのパターンとしては,ランダムパターンやフレネルゾーンプレート(空間的チャープ信号:場所によって周波数の変化する信号)等が用いられる。これらは,その自己相関関数がほぽディラックのδ関数で近似できるという特徴をもっており,再構成にはこの性質を利用するのである。

図2 M配列符号化開口
(4×4周期のM配列を鉛板に孔を開けて作成した)
筆者らが用いたランダムパターンは,M系列と呼ばれる疑似乱数系列を2次元に配置したM配列である(図2)。このパターンの自己相関関数を図3に示すが,これは他のパターンに比較して著しい特徴がある。それは,ピークが1箇所にのみ存在し,それ以外の場所では一定の値を取るということである。他のランダムパターンやフレネタソーンプレートでは,大きいピークは1箇所ではあるがそれ以外に小さな凹凸が多数生じ,再構成の際の偽像(ゴースト)の原因となる。ただ,M配列はある規則にしたがって生成されるため,一定周期で繰り返されるという性質があり,このための不都合が生じる。しかし,この不都合の性質も予め知ることができるので,それを避けることができる。
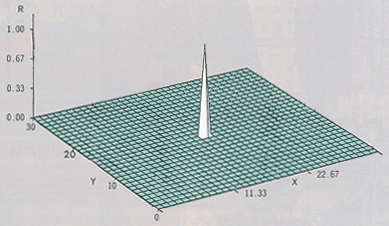
図3 M配列(1周期分)の自己相関関数
再構成においては,まず,開口からある距離にある断面を考える。この距離が決まれば,そこに放射源が存在すれば,それによる陰の大きさ(倍率M)が決まる。符号化開口のパターンをM倍したものと,観測で得られた投影データとの2次元相関関数を計算する。もし,この面に放射源が一個だけ存在したとすれば,そのときの相関関数の形は丁度図3のようになる。ここで,ピークの位置が放射源の位置に対応する。複数個放射源が存在すれば,それぞれの位置にピークが現われる。この計算を,考える断面の開口からの距離を変えながら,実行すると,それぞれの断面での放射源の分布が得られるので,結局3次元分布が求まることになる。
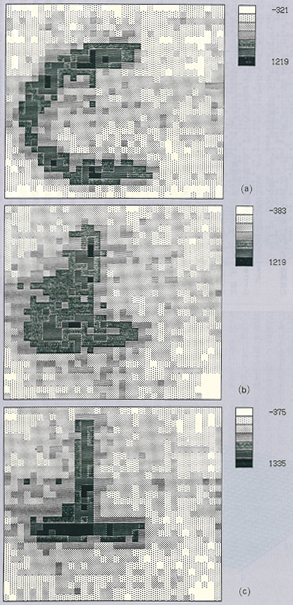
図4 再構成像の例
実際にこうして得た結果を図4(a)~(c)に示す。これは,CとTという文字の形に切り抜いた吸い取り紙にテクネチウムを染み込ませたものを,開口から,それぞれ,29cm,43cmの位置に置き,符号化開口を通してシンチレーションカメラで観測して得たデータから,上で述べた方法で再構成して得た結果である(再構成面:図(a):26cm,図(b):33cm,図(c):49cm)。
仮定した断面が実際に放射源の存在する面か,その面の極く近傍であれば(図(a),(c)),放射源の分布がほぼ正確に再生できることが分かる。図4(b)から,実際には放射源の存在しない面にもあたかも放射源が存在するかのごとき結果が得られていることが分かる。これが,符号化開口形の欠点である。
こういうことが生じるのは,相関関数の性質によっている。つまり,僅かに倍率の異なる開口パターン間の相関関数がゼロにはならないため,上の相関関数の計算において,想定する断面が実際に放射源の存在する面に近ければ,投影に含まれている開口の陰と,倍率の僅かに異なる符号化開口との相関関数が計算されることとなり,その値がゼロではない値を取ることになるからである。
これをできるだけゼロに近付けるには,測定系において,(1)開口のピッチを小さくする,(2)開口を構成する孔を小さくする,(3)検出面積を大きくする,(4)元々の倍率を大きくするなどが必要である。しかし,これらを直接的に実現しようとすると,S/Nの低下を招いたり,装置が複雑で高価になったりして符号化開口形の長所が損なわれる。複数投影を利用して,実効的にこれらを実現する工夫を行ってよい結果を得つつある。これらは,差動形と両眼視(立体視)形で,それぞれ,
(I)差動形:開口孔を小さくすること(2)に相当するが,実際に孔を小さくすることはS/Nの低下を招く。観測において,最初の投影を得た後,検出器あるいは開口を奥行き方向に僅かにずらせてもう一度投影を得る。両者の差を基にして再構成を行うと,S/Nを低下させずに,実効的に孔を小さくしたのと同様の効果が実現できる,
(II)両眼視形:検出面積を大きくすること(3)は検出器を大きくすることになり,現実には実現が困難である。検出器を大きくすることなく,最初の投影を得た後,検出器面内で検出器を僅かに移動して(あるいは,面内に2個の面検出器を並べて)検出することにより,実効的に検出面積を大きくできる,
というものである。
さらに,像再構成系においても,再構成の演算に反復法を用いて分解能の向上を図っている。これは,再構成した分布を再度投影し,観測された投影データに近付くように繰り返し演算を行うことにより,元来放射源の存在しない断面に演算によって再生される放射源を少なくすることで分解能の向上を図るものであるが,詳細は別の機会に譲る。
おわりに
放射線を利用した医用画像解析の内,現在最も関心を集めているCT技術について,極く概略を紹介し,その一つの方法である符号化開口放射形CTについて,その原理,結果,問題点等を示し,問題点を解決する考え方を述べた。符号化開口ECTは,簡便であってしかも3次元分布の情報が,限られた方向からの観測,限られた数の投影から得られるという極めて大きい特徴をもつ。分解能の向上が実現されれば実用上も大きな意義を有する。なお,定量的な情報を得るには,さらに,光路中の吸収・散乱に対する補正も必要になる。一方,光路中の吸収や,回折,散乱,また,開口による回折の影響などをモデル化して再構成のアルゴリズムに含ませれば,放射線に限らず他の放射源分布の測定に拡張することも可能である。医療で用いられるCTにはこの他にも核磁気共鳴を利用するMRI(Magnetic Resonance Imaging)や超音波を用いるCTなどがある。このように,CT技術は放射線に限らず他の放射や波動に拡張されたり,医療に限らず産業計測など他の分野にも拡張される傾向にあり,その面での進展も大いに期待されるところである。



