Accumu Vol.16
天津にて
京都情報大学院大学教授 作花 一志

写真1
2007年8月24日から9月15日まで3週間,中国の天津へ出張してきました。すでに恒例となった提携校である天津科技大学国際学院で集中講義,今年の夏には筆者に番が回ってきて,インターンシップの5人の若き講師と一緒です。4年半ぶりに訪れた天津はオリンピックを来年に控え急ピッチで変容していて,大学のインターネット環境も大幅に改善されていました。
筆者のこの度の担当科目は3回生対象の「データベース入門」です。正規化とSQLの解説が主眼で,Accessで実習を行いました。8月27日,新学期が始まり,8時から始まる1時間目は51名中,遅刻欠席者なしという日本ではまず見られない出席状態です。最初の授業で全員に日本語で自己紹介をしてもらいました。趣味はサッカーと日本の漫画・アニメ,そして日本へ行きたいという学生が多いのが印象的でした。授業は毎日8時,10時,14時,16時から100分(途中に休憩あり)行われ,夜間もあります。ITと日本語が2大重要科目のようで,2・3回生はなんと週に22時限受講しているそうです。しかも各科目とも5回欠席したら単位は取れないという厳しい状況ですが,学生は素直・勤勉で日本の学生より若く見えます。日本語専攻の学生なので,授業は日本語で行われますが,上級生のTAが適宜翻訳してくれます。実習のレポートはまずまずのできばえでしたが,試験の問題を日本語で答えるのはやはり難しいようでした。
写真1は9月13日に最終授業が終わって記念の集合写真です。9月10日は「教師の日」だそうで,学生から花とメッセージカードを贈られました。中国ではその日は母の日,父の日と並んで重要な感謝の日らしいです。でもなぜ9・10か,国際学院の先生方に尋ねてみましたが,その起源はご存じないようでした。夜はパーティーがあり招待されました。日米豪からの先生たちが多数参加して歓談の時を過ごしました。

写真2
ところで天津市は直轄都市で中国第3の大都市で,人口も面積も京都府と大阪府を合わせたくらいあります。北京から高速バスで2時間半の途中は,高い山はなく,ただただ広大な平坦な黄色の大地でした。この広大な平地は一体何に使われているのだろう? 窓から見たところ背の低い樹木だけで,農地でもなく宅地でもない広大な平地ということ自体が不思議でした。日本では狭い平地は100%使われていますね。天津では雨に遭ったのは3週間のうち2回だけという乾燥地帯ですが,青い空,白い雲,緑の山は見られず,いつも靄のかかっているような空でした。特に夜空に星が見えなかったのは寂しかった。9月8日には国際学院の先生たちに連れられて北京観光へ行きました。北京北部の八達嶺は今や観光客でいっぱいです(写真2)。総延長は延々6300km(~地球の半径)に及び,ユネスコの世界遺産(文化遺産)にも登録され「月から見える唯一の建造物」とも言われています。秦の始皇帝から明まで改修を重ね1800年間もかかって築き上げたそうです。すなわち中国は4000年の歴史のうちの三分の一をこれに費やし, 兵士たちは戦をするより土木工事をするほうが多かったわけです。レンガ造りで頑丈に見えますが,北方民族はこの長城を越えて幾度となく中国内部に侵入しているところをみると,防御壁としての効果は疑問です。

写真3
大学の構内で写真3のような胸像に出会いました。「祖冲之ってどこかで聞いたことがあるな?」と思い調べてみると1500年前,南北朝時代の数学者で,円周率を詳しく計算したことで有名な人です(430ー501)。 円の周囲の長さと直径の比は3.14159265…とどこまでも不規則に続く数であることは今日誰もが知っていますが,その算出には紀元前からの歴史があります。ギリシアではアルキメデス(紀元前3世紀)やプトレマイオス(2世紀)たちがすでに3.14という値を求めているそうです。中国でも張衡(2世紀)や劉徽(3世紀)たちが同様な計算をしています。祖冲之の求めた値は現在のものと比べ3.141592まで正確で,1500年前としては世界の最高レベルでした。ヨーロッパでこれより詳しい値が知られたのは16世紀になってから,すなわち祖冲之は1000年以上も世界最高記録を持っていたことになります。今日のような数字も数式もない,もちろん計算道具もない時代に彼はどんな方法で計算したのでしょうか?半径0.5の円に内接する正6角形の周囲の長さは3で,正8角形,正12角形,正16角形…としていけば次第に正確な値に近づきますが,彼の値を求めるにはなんと正24576角形を描かねばならないそうです。
祖冲之の役職は「太史令」という天文官かつ歴史官です。古代中国では人民に時を知らせることは皇帝の重要な仕事であり,そのため暦の作成・配布のために専属の官吏が任命されていました。彼らはカレンダーを作るだけでなく,日食・月食・惑星運行の記録や予報も行っています。日食予報をサボったためクビになった(解雇ではなく死刑)天文官の話が史書に残っています。さらに占いもしましたが,今のように個人の金運・愛情運というものではなく,国家の安泰・王朝の命運を占ったのです。また歴史の編纂もします。かの大歴史学者である司馬遷(紀元前145ー同87)も漢の太史令でした。当時の天文学者の仕事は命がけで,星空を眺める余裕はなかったでしょうね。
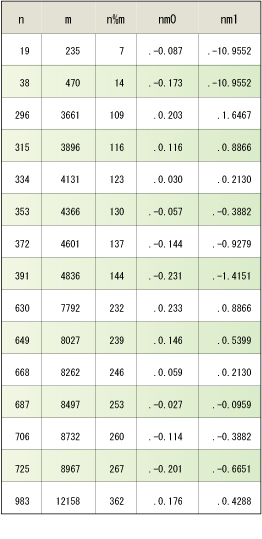
彼の業績は「大明暦」を作ったことです。暦を作るのに面倒なのは端数の問題です。1年は365.242194…日,1月は29.530589…日,その比は12.36842…,どうしてもきれいな整数比になりません。したがって,何年かに何度かは閏月をおいて1年13月としなければならないのです。それには12.36842…に近い分数をさがすことで,もっとも簡単なのでも235/19です。この数値はすでに約2400年前に中国とギリシアで独立に知られていました。すなわち19年が235月で,235=19×12+7だから19年に7回ほど閏月を置くというもので,中国では「章」,ギリシアでは「メトンの周期」と呼ばれていました。ところがこれでは100年もすると半日の誤差がでるので,祖冲之は4836/391という値を見つけました。4836=391×12+144だから391年間に144回閏月を置くということになります。実際こうすれば数百年間で誤差は数時間以内に収まります。この暦は作成が難しかったせいか,採用されたのは彼が亡くなって50年後のことでした。他にどんな分数があるのか,実際に計算してみた結果が表です。n太陽年とm朔望月をほぼ等しいとして,求める分数はm/nで,第3欄n%mはこのn年間に置くべき閏月の回数,次nm0はこのn年とm月の誤差(日),そしてnm1は100年間の誤差(時)を表しています。最も誤差が少ないのは334年間に123回閏月を置くというものです。今でこそ余りと2重ループとIf文の演習問題ですが,まともにやるとPCが停まってしまいますから要注意です。円周率といい暦といい,彼はよっぽど計算達者だったのでしょう。果たしてどんなアルゴリズムを使ったのか? これらは彼の『綴術』という著書に書いてあるそうですが,残っていません。
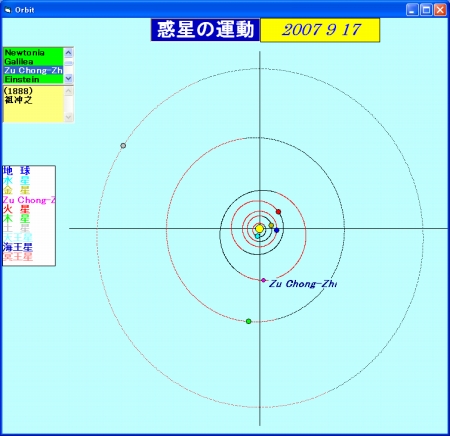
図1
帰国してから彼の名がついた小惑星があることがわかりました。実は学生が調べてメールで知らせてくれたのです。それは(1888)ZuChong-Zhi,祖冲之の中国語読みです。早速,軌道要素を調べると火星と木星の間にあり,太陽の周りを約4年で公転しています。図1は2007年9月17日の惑星配置で,木星と同方向,さそり座にあります。軌道線は内側から水星・金星・地球・火星・ZuChong-Zhi・木星・土星です。さらに彼の名がついている月のクレータがありTsu Chung-Chiという名で登録されていることがわかりました。小惑星にも月にも名づけられたというと,コペルニクスやケプラーなみの大天文学者と評価すべきなのでしょうか。ともあれ,中国でこのような人と出会えたことは幸運でした。
なおこの小文はKCGブログに載った私の記事をまとめたものです。



