Accumu Vol.1
恒星の固有運動
作花 一志
私達の先祖は文明の始まりと共に天体の観測を始め,星の運行より宇宙の法則と人間の運命を知ろうと努めてきた。古代の人々が種を播き穂を取り入れるとき,海を渡り砂漠を旅するとき天文学は彼らに貴重な指針を与えた。夜空に光る星はわずかの惑星・彗星等を除けばすべてお互いに位置を変えぬ恒星で,それは1日1回転する天球に固定されているものと考えられていた。しかし地動説の確立と共に天球は実体を失い,恒星は太陽系とは全く独立な天体であることがわかってきた。恒星もまた不動な天体ではなく長い年月の間にはその動きが認められるはずであるが,それを観測するには人間の歴史はあまりにも短い。現在私達は太陽も含めすべての恒星は個々の運動をしながらも全体としては銀河中心のまわりを回転していることを知っている。恒星の動きは毎秒数十kmというスピードであるが,私達から見て1年間に角度の1秒にも満たない。これは当然恒星が私達の日常感覚からするとあまりにも遠方にあるからである。
この小文では数十光年(約100兆km),数十万年のオーダーの空間的・時間的広がりの世界の中で恒星の太陽に対する運動を調べ,位置・距離・明るさの変化の計算結果を示そう。
恒星とは自ら光る星であるが,エネルギーを四方八方宇宙空間へ放出しているのであるから当然いつかは寿命が尽きてしまう。その寿命は典型的な(大き過ぎもなく小さ過ぎもなく,明る過ぎもなく暗過ぎもなく,全く平凡な)恒星である太陽で約100億年で,質量が大きいほどエネルギーを浪費し短命となり,数百万年で燃え尽きてしまう星もある。星はその晩年,何十倍も膨張し急に明るさを増したり,激しく変光したりするが,通常夜空に輝いている大多数の星は安定な状態にあり,数十万年の間で星の本来の明るさが変わることは考えなくてよい。天体の明るさは等級(mag.)を単位に用い明るさ100倍の違いが5等級の差と定義され,観測より0.01mag.の精度で求められている。
天体の距離には単位として光年(ly)を使う。1lyは光が1年間に進む距離で約1013kmで最も近い恒星(ケンタウルス座α星)で4.3lyである。恒星の距離の測定は地球の公転運動による恒星の見かけの運動を追跡することによって得られるが,200ly以遠の恒星では当然精度は悪くなる。
天体の位置は赤経α,赤緯δで表わされるがこれは,地球の経度,緯度に相当する天球上の座標である。各天体の(α,δ)は望遠鏡発明以前から調べられており,今日では観測できる天体(恒星,惑星,彗星,星雲,星団,銀河……)はすべて各々のカタログに収められている。
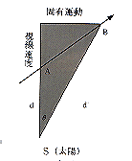
図1
恒星の運動は私達への視線方向とそれに直角方向があるが,前者を視線速度,後者を固有運動という。(図1参照)視線速度はスペクトル写真を撮って初めてわかる。望遠鏡のお尻に分光装置(プリズムまたは回折格子など)を着け弱い光を増幅して写真乾板上に情報を焼き付ける。近づいてくる光源ではスペクトル線が本来の波長より短波長側(青方)へ,遠ざかる光源では長波長側(赤方)へずれるというドップラー効果を利用し,スペクトル線の本来の波長からのシフト量を測れば視線速度は求まる。実はこのズレはわずか20~30ミクロンなのでこの測定の際には「顕微鏡」を用いる。
視線速度(Rkm/s) 本来の波長からのズレ
―――――――――――― = ――――――――――
光速(3.0×105km/s) 本来の波長
R>0とは遠ざかることを,R<0とは近づくことを表す。
一方固有運動は長い年月をかけて直接写真を何枚も撮り,星の位置を精密に測定することによって得られるが,この測定には誤差1ミクロン程度の精度を要し視線速度の場合に比べ非常に困難である。1年間に恒星が移動した角度をμ″,その赤経方向成分をμ1″,赤緯方向成分をμ2″,μの位置角をφとしよう。
tanφ=μ1/μ2(0°≦φ<360°)
μ2=μ12+μ22
恒星の位置,明るさ,固有運動,視線速度,距離の値を「理科年表」より取って距離,明るさ,位置の変化を調べよう。一定速度(視線速度R,固有運動μ)で運動している恒星がy万年後に図1のA点よりB点へ移動し,距離はd光年からd′光年に変わったとする。
∠ASB=θとすると
d′sinθ=4.848μdy×10-2
d′cosθ=d+3.336Ry×10-2
が成り立ちこれよりd′が求まる。距離が変われば当然明るさが変わり,次式によりm等級よりm′等級となる。
m′=m+5logd/d′
赤経,赤緯は(α,δ)より(α′,δ′)へ移る。
cosδ′sin(α′-α)=sinθ sinφ
cosδ′cos(α′-α)=cosδ cosθ-sinδ sinθ cosφ
sinδ′=sinδ cosθ+cosδ sinθ cosφ
これらの式を使って,α,δ,μ1,μ2,m,d,Rを与えd′,m′,α′,δ′を本学院実習用のパソコンで計算した。例としてベガ(織女星)とアルタイル(彦星)の距離と明るさを5万年毎にプロットした結果が図2,図3に示されている。1目盛りは横軸では10万年,縦軸では10光年(距離)および1等級(明るさ)である。ベガは現在26光年の彼方より14km/sの速さで近づいており,約30万年後に最も近づき(18光年),その時は現在より約1等級明るくなる。またアルタイルは14万年後には現在の距離の半分あたりまで近づきベガより明るく輝く。両星の距離は現在15.3光年であるが7万年後に15.0光年まで近づきその後は永遠に離れてゆくばかりである。残念ながら七夕の2人の一夜の逢瀬はかなえられそうにない。またカペラ(馭者座の主星)は現在遠ざかりつつあり太陽最接近時を逆算すると約20万年前だったということになる。(図4)。

図2
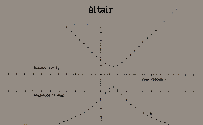
図3
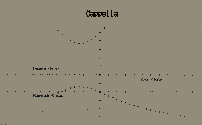
図4
これらの運動の結果,星座の形も変わってゆき,数十万年後には今の夜空とは似ても似つかぬものになってしまう。北斗七星の両端の星は他の5つの星より固有運動が大きく,図5~図9のように形はどんどん崩れてゆく。そして10万年後には逆向けのひしゃく型になるだろう。そのころの天にはオリオンもさそりもししも見られない。

図5 -10万年後の北斗七星

図6 -5万年後の北斗七星

図7 0万年後の北斗七星

図8 5万年後の北斗七星

図9 10万年後の北斗七星
私達の歴史はまだ数千年でしかなくこの間に恒星が移動した距離は1光年にも満たず,天球上の動きは数度でしかない。しかしネアンデルタール人は私達とは異なった星座を見ていたはずだし,数十万年後人類が生き延びられたら私達の子孫は今と全く違った星の物語を語り合っているだろう。



